题目内容
3.函数y=sinx-$\sqrt{3}$cosx+1的值域为[-1,3].分析 由条件利用两角和的正弦公式求得函数的解析式,再利用正弦函数的值域求得f(x)的值域.
解答 解:函数y=sinx-$\sqrt{3}$cosx+1=2($\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$cosx)+1=2sin(x-$\frac{π}{3}$)+1,
故函数的值域为[-1,3],
故答案为:[-1,3].
点评 本题主要考查两角和的正弦公式、正弦函数的值域,属于基础题.

练习册系列答案
相关题目
18.设X为随机变量,X~B (n,$\frac{1}{3}$),若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
| A. | $\frac{80}{243}$ | B. | $\frac{13}{243}$ | C. | $\frac{4}{243}$ | D. | $\frac{13}{16}$ |
8.设函数f(x)=-2x2+4x在区间[m,n]上的值域是[-6,2],则m+n的取值所组成的集合为( )
| A. | [0,3] | B. | [0,4] | C. | [-1,3] | D. | [1,4] |
15.如图是某三棱锥的三视图,则该三棱锥的表面积为( )
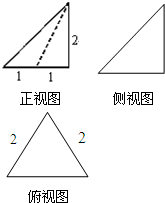

| A. | 4+$\sqrt{7}+\sqrt{3}$ | B. | 6+$\sqrt{7}$ | C. | 4+$\sqrt{7}$ | D. | 6+$\sqrt{3}$ |