题目内容
7．用反证法证明命题：“三个连续正整数a，b，c中至少有一个能被2整除”时，要做的假设是（ ）| A． | 假设三个连续正整数a，b，c都不能被2整除 | |
| B． | 假设三个连续正整数a，b，c都能被2整除 | |
| C． | 假设三个连续正整数a，b，c至多有一个能被2整除 | |
| D． | 假设三个连续正整数a，b，c至多有两个能被2整除 |
分析 写出要证明命题的否定，即为所求．
解答 解：根据用反证法证明数学命题的步骤，应先假设要证命题的否定成立，
而要证命题的否定为：“三个连续正整数a，b，c都不能被2整除”，
故选：A．
点评 本题主要考查用反证法证明数学命题的方法和步骤，求一个命题的否定，属于中档题．
练习册系列答案
相关题目
18．设X为随机变量，X～B （n，$\frac{1}{3}$），若随机变量X的数学期望E（X）=2，则P（X=2）等于（ ）
| A． | $\frac{80}{243}$ | B． | $\frac{13}{243}$ | C． | $\frac{4}{243}$ | D． | $\frac{13}{16}$ |
15．如图是某三棱锥的三视图，则该三棱锥的表面积为（ ）
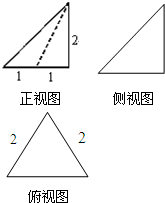
| A． | 4+$\sqrt{7}+\sqrt{3}$ | B． | 6+$\sqrt{7}$ | C． | 4+$\sqrt{7}$ | D． | 6+$\sqrt{3}$ |
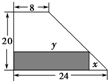某厂有许多形状为直角梯形的铁皮边角料，如图，为降低消耗，开源节流，现要从这些边角料上截取矩形铁片（如图中阴影部分）备用，当截取的矩形面积最大时，矩形两边长x、y应为15，12．