题目内容
17.函数f(x)=log2x+2x-6的零点一定位于下列哪个区间( )| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
分析 函数f(x)=log2x+2x-6在其定义域上连续,同时可判断f(2)<0,f(3)>0;从而判断.
解答 解:函数f(x)=log2x+2x-6在其定义域上连续,
f(2)=log22+2•2-6=-1<0,
f(3)=log23+2•3-6=log23>0;
故函数f(x)=log2x+2x-6的零点在区间(2,3)上,
故选B.
点评 本题考查了函数的零点的判断与应用,属于基础题.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
8.设函数f(x)=-2x2+4x在区间[m,n]上的值域是[-6,2],则m+n的取值所组成的集合为( )
| A. | [0,3] | B. | [0,4] | C. | [-1,3] | D. | [1,4] |
5.若动点P在直线l1:x-y-2=0上,动点Q在直线l2:x-y-6=0上,设线段PQ的中点M(a,b),满足a2+b2-4a+4b≤0,则a2+b2的取值范围是( )
| A. | [2$\sqrt{2}$,4] | B. | [2$\sqrt{2}$,2$\sqrt{3}$] | C. | [8,12] | D. | [8,16] |
2.为调查某养老院是否需要志愿服务者提供帮助的情况,用简单随机抽样的方法选取了16名男性和14名女性进行调查,调查发现,男、女中分别有10人和6人需要志愿者提供帮助.
(Ⅰ)根据以上数据完成以下2×2列联表:
(Ⅱ)能否在犯错的概率不超过0.10的前提下推断性别与需要志愿者提供帮助有关?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
(Ⅰ)根据以上数据完成以下2×2列联表:
| 需要 | 不需要 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| K0 | 0.708 | 1.323 | 2.706 | 6.635 |
6.曲线y=ln(x-1)上的点到直线x-y+4=0的最短距离是( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
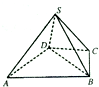 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.