题目内容
1.已知函数f(x)=$\frac{x+a}{{e}^{x}}$(a∈R,其中e≈2.71828…),记f′(x)为函数f(x)的导函数.(Ⅰ)若曲线y=f(x)在x=0处的切线与直线x+y=0平行,求a的值;
(Ⅱ)求函数f(x)在[-2,+∞)上的最大值;
(Ⅲ)若a=-1,令an=f′(n),n∈N+,证明:-252<a1+a2+a3+…+a2018<$\frac{1}{2}$.
分析 (Ⅰ)由求导公式和法则求出f′(x),在点(1,f(1))处的切线与x+y=0平行得:f′(1)=-1,求出a的值;
(Ⅱ)由f′(x)=0求出临界点是x=1-a,根据1-a与-2的大小关系进行分类讨论,分别判断出导数的符号,可求出函数的单调区间;
(Ⅲ)把a=-1代入f′(x)化简,令g(x)=f′(x)并求出g′(x),求出g(x)的单调区间和最小值,利用单调性求出f′(n)的范围,再由放缩法证明结论成立.
解答 解:(Ⅰ)解:由题意得,f′(x)=$\frac{{e}^{x}-(a+x){e}^{x}}{{(e}^{x})^{2}}$=$\frac{1-a-x}{{e}^{x}}$,…(2分)
∵在x=0处的切线与直线x+y=0平行,
∴f′(0)=1-a=-1,解得a=2; …(3分)
(Ⅱ)令f′(x)=$\frac{1-a-x}{{e}^{x}}$=0,得x=1-a,…(4分)
①当a≥3时,在x∈[-2,+∞)上,f′(x)≤0,
∴f(x)在[-2,+∞)上单调递减,
∴f(x)的最大值是f(-2)=e2(a-2); …(5分)
②当a<3时,
当x∈[-2,1-a)时,f′(x)>0,f(x)在[-2,1-a)上单调递增;
当x∈[1-a,+∞)时,f′(x)≤0,f(x)在[1-a,+∞)上单调递减,
∴f(x)的最大值是f(1-a)=ea-1; …(7分)
证明:(Ⅲ)当a=-1时,令g(x)=f′(x)=$\frac{2-x}{{e}^{x}}$,则$g′(x)=\frac{x-3}{{e}^{x}}$,
当x>3时,g′(x)>0,∴g(x)在(3,+∞)上单调递增,
当0<x<3时,g′(x)<0,∴g(x)在(0,3)上单调递减,…(8分)
∴f′(x)的最小值是f′(3)=$-\frac{1}{{e}^{3}}$,
∵x>3时,g(x)=f′(x)=$\frac{2-x}{{e}^{x}}<0$,…(9分)
当n>3时,$-\frac{1}{{e}^{3}}$<f′(n)<0,
∴$-\frac{2016}{{e}^{3}}$<a1+a2+a3+…+a2018<0,…(10分)
又a1=f′(1)=$\frac{1}{e}$,a2=f′(2)=0,
∴$\frac{1}{e}-\frac{2016}{{e}^{3}}$<a1+a2+a3+…+a2018<$\frac{1}{e}$,
又∵$\frac{1}{e}-\frac{2016}{{e}^{3}}$>$\frac{1}{e}-\frac{2016}{{2}^{3}}$=$\frac{1}{e}-252>-252$,$\frac{1}{e}<\frac{1}{2}$,
∴-252<a1+a2+a3+…+a2018<$\frac{1}{2}$,即命题成立. …(12分)
点评 本题考查导数的几何意义,导数与函数的单调性、极值、最值的关系,利用数列的单调性和放缩法证明不等式,考查分类讨论思想,化简、变形能力,综合性大、难度大.

| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
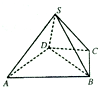 如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.
如图,四棱锥S-ABCD中,△ABD是正三角形,CB=CD,SC⊥BD.