题目内容
已知直线ax＋by－1＝0(a，b不全为0)与圆x2＋y2＝50有公共点，且公共点的横、纵坐标均为整数，那么这样的直线共有 （ ）
| A．66条 | B．72条 |
| C．74条 | D．78条 |
B
当
时，圆上横、纵坐标均为整数的点有
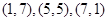，根据题意画出图形，如图所示：
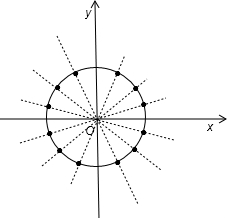
根据圆的对称性得到圆上共有3×4=12个点横纵坐标均为整数，经过其中任意两点的割线有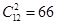
条，过每一点的切线共有12条，上述直线中经过原点的有6条，如图所示，则满足题意的直线共有66+12-6=72条．故选B
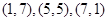时，圆上横、纵坐标均为整数的点有，根据题意画出图形，如图所示：根据圆的对称性得到圆上共有3×4=12个点横纵坐标均为整数，经过其中任意两点的割线有
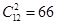条，过每一点的切线共有12条，上述直线中经过原点的有6条，如图所示，则满足题意的直线共有66+12-6=72条．故选B
练习册系列答案
相关题目
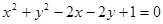相切的直线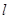
交x轴、y轴于A、B两点，O为原点，|OA|=3，|OB|=b(b>2).
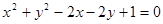上的点到直线
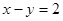的距离最小值是（ ）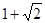
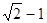
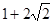
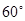的直线被圆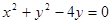
所截得的弦长为（ ）
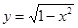和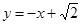
公共点的个数为（ ）
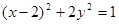上，则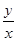
的最大值为( )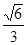
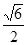
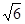
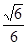
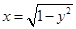与直线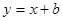
有两个交点，则
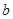的取值范围是 .
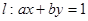与圆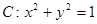
有两个不同的交点， 则点
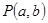与圆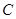
的位置关系是