题目内容
15.已知f(x)=x2-ax,g(x)=lnx,h(x)=f(x)+g(x).(1)当a=3时,求h(x)的单调区间;
(2)设h(x)有两个极值点x1,x2,且x1∈(0,$\frac{1}{2}$),若h(x1)-h(x2)>m恒成立,求m的最大值.
分析 (1)将a=3代入函数的表达式,求出函数h(x)的导数,从而得到函数的单调区间;
(2)求出h′(x),根据h(x)=f(x)+g(x)有两个极值点x1,x2,可以确定x1,x2为h′(x)=0的两个根,从而得到x1x2=$\frac{1}{2}$,可以确定x2>1,求解h(x1)-h(x2),构造函数u(x)=x2-$\frac{1}{{4x}^{2}}$-ln2x2,x≥1,利用导数研究u(x)的取值范围,从而可以证得h(x1)-h(x2)>$\frac{3}{4}$-ln2,进而求出m的最大值.
解答 解:(1)a=3时,h(x)=x2-3x+lnx,
h′(x)=2x-3+$\frac{1}{x}$=$\frac{{2x}^{2}-3x+1}{x}$=$\frac{(2x-1)(x-1)}{x}$,(x>0),
令h′(x)>0,解得:x>1或0<x<$\frac{1}{2}$,令h′(x)<0,解得:$\frac{1}{2}$<x<1,
∴h(x)在(0,$\frac{1}{2}$),(1,+∞)递增,在($\frac{1}{2}$,1)递减;
(2)∵h(x)=f(x)+g(x)=x2-ax+lnx,
∴h′(x)=$\frac{{2x}^{2}-ax+1}{x}$,(x>0),
∵h(x)=f(x)+g(x)有两个极值点x1,x2,
∴x1,x2为h′(x)=0的两个根,即2x2-ax+1=0的两个根,
∴x1x2=$\frac{1}{2}$,
∵x1∈(0,$\frac{1}{2}$),
∴x2∈(1,+∞),且axi=2${{x}_{i}}^{2}$+1(i=1,2),
∴h(x1)-h(x2)=(${{x}_{1}}^{2}$-ax1+lnx1)-(${{x}_{2}}^{2}$-ax2+lnx2)
=${{x}_{2}}^{2}$-${{x}_{1}}^{2}$+ln$\frac{{x}_{1}}{{x}_{2}}$=${{x}_{2}}^{2}$-$\frac{1}{{{4x}_{2}}^{2}}$-ln2${{x}_{2}}^{2}$,(x2>1),
设u(x)=x2-$\frac{1}{{4x}^{2}}$-ln2x2,x≥1,
∴u′(x)=$\frac{{({2x}^{2}-1)}^{2}}{{2x}^{3}}$≥0,
∴u(x)>u(1)=$\frac{3}{4}$-ln2,
∴h(x1)-h(x2)>$\frac{3}{4}$-ln2,
∴m≤$\frac{3}{4}$-ln2,
∴m的最大值是:$\frac{3}{4}$-ln2.
点评 本题考查了函数的单调性问题,考查导数的应用,一般导数的正负对应着函数的单调性.利用导数研究函数在闭区间上的最值,一般是求出导函数对应方程的根,然后求出跟对应的函数值,区间端点的函数值,然后比较大小即可得到函数在闭区间上的最值,属于难题.

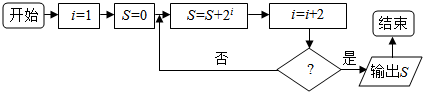
| A. | i≥7 | B. | i>9 | C. | i≥9 | D. | i>10 |
| A. | (2,1) | B. | (1,2) | C. | (-1,-2) | D. | (2,-1) |
| A. | $\frac{1}{ab}>\frac{1}{2}$ | B. | a2+b2≥8 | C. | $\sqrt{ab}$≥2 | D. | $\frac{1}{a}+\frac{1}{b}$≤1 |
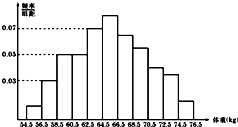 为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.
为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.