题目内容
5.已知函数f(x)=x3-3ax-1(a∈R)(1)试讨论函数f(x)的单调区间;
(2)若f(x)=0在x∈[0,1]上恒成立,求a的取值范围.
分析 (1)先求出函数的导数,题干讨论a的范围,得到函数的单调性,从而求出其单调区间;(2)题干讨论a的范围结合函数的单调性得到不等式,解出即可.
解答 解:(1)f′(x)=3x2-3a,
当a≤0时,f′(x)≥0,
∴函数f(x)在(-∞,+∞)单调递增,
当a>0时,由f′(x)>0,解得:x<-$\sqrt{a}$或x>$\sqrt{a}$,
f′(x)<0,解得:-$\sqrt{a}$<x<$\sqrt{a}$,
∴函数f(x)在(-∞,-$\sqrt{a}$)递增,在(-$\sqrt{a}$,$\sqrt{a}$)递减,在($\sqrt{a}$,+∞)递增;
(2)由(1)得:
当a≤0时,f(x)在[0,1]递增,∴f(x)≤f(1),
∴满足f(1)≤0即可,解得:a=0,
当0<a<1时,f(x)在[0,$\sqrt{a}$]递减,在[$\sqrt{a}$,1]递增,
∴满足$\left\{\begin{array}{l}{f(0)≤0}\\{f(1)≤0}\end{array}\right.$即可,解得:0<a<1,
当a≥1时,f(x)在[0,1]上单调递减,f(x)≤f(0),
∴f(x)≤0恒成立,
故实数a的范围是[0,+∞).
点评 本题考查了函数的单调性问题,考查导数的应用,分类讨论思想,是一道中档题.

练习册系列答案
相关题目
16.“直线l垂直于平面α内两直线a,b”是“直线l⊥平面α”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.已知数列{an}满足a1=0,an+1=an+2n,则a2016等于( )
| A. | 2016×2 017 | B. | 2015×2 016 | C. | 2014×2 015 | D. | 2016×2 016 |
15.在一次某班42名学生参加课外篮球、排球兴趣小组(每人参加且只参加一个兴趣小组)的情况调查中,经统计得到如下2×2列联表:(单位:人)
通过计算得x2=4.852,则参加“篮球小组”与性别间有关系的可能性为( )
(下面临界值表供参考
| 篮球 | 排球 | 总计 | |
| 男同学 | 16 | 6 | 22 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 24 | 18 | 42 |
(下面临界值表供参考
| P(x2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
| A. | 99% | B. | 95% | C. | 90% | D. | 无关系 |
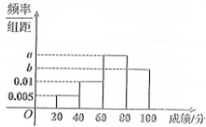 某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.
某班的全体学生(共50人)参加数学测试(百分制),成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],依此表可以估计这次测试成绩的中位数为70分.