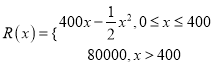题目内容
【题目】如图,几何体是圆柱的一部分,它是由矩形![]() (及其内部)以
(及其内部)以![]() 边所在直线为旋转轴旋转
边所在直线为旋转轴旋转![]() 得到的,
得到的, ![]() 是
是![]() 的中点.
的中点.
(![]() )设
)设![]() 是
是![]() 上的一点,且
上的一点,且![]() ,求
,求![]() 的大小;
的大小;
(![]() )当
)当![]() 时,求二面角
时,求二面角![]() 的大小.
的大小.

【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)由已知利用线面垂直的判定可得BE⊥平面ABP,得到BE⊥BP,结合∠EBC=120°求得∠CBP=30°;
(Ⅱ).以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.求出A,E,G,C的坐标,进一步求出平面AEG与平面ACG的一个法向量,由两法向量所成角的余弦值可得二面角E-AG-C的大小.
试题解析:
(Ⅰ)因为![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,
,
因此![]()

(Ⅱ)以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() ,
, ![]() 所在的直线为
所在的直线为![]() ,
, ![]() ,
, ![]() 轴,建立如图所示的空间直角坐标系.由题意得
轴,建立如图所示的空间直角坐标系.由题意得![]()
![]() ,
, ![]() ,
, ![]() ,故
,故![]() ,
, ![]() ,
, ![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
由 可得
可得
取![]() ,可得平面
,可得平面![]() 的一个法向量
的一个法向量![]() .
.
设![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
由 可得
可得
取![]() ,可得平面
,可得平面![]() 的一个法向量
的一个法向量![]() .
.
所以![]() .
.
因此所求的角为![]() .
.

练习册系列答案
相关题目
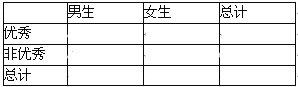
【题目】大家知道, 莫言是中国首位获得诺贝尔奖的文学家, 国人欢欣鼓舞.某高校文学社从男女生中各抽取![]() 名同学调查对莫言作品的了解程度, 结果如下:
名同学调查对莫言作品的了解程度, 结果如下:
阅读过莫言的作品数( 篇) |
|
|
|
|
|
男生 |
|
|
|
|
|
女生 |
|
|
|
|
|
(1)试估计该校学生阅读莫言作品超过![]() 篇的概率;
篇的概率;
(2)对莫言作品阅读超过![]() 篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过
篇的则称为“对莫言作品非常了解” , 否则为“ 一般了解” .根据题意完成下表, 并判断能否在犯错误的概率不超过![]() 的前提下, 认为对莫言作品非常了解与性别有关?
的前提下, 认为对莫言作品非常了解与性别有关?
非常了解 | 一般了解 | 合计 | |
男生 | |||
女生 | |||
合计 |
附: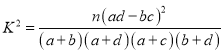 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|