题目内容
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
![]()
表2:女生
![]()
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
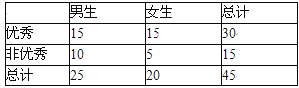
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.

参考数据与公式:
K2=![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
![]()
【答案】(1)![]() ;(2)没有
;(2)没有![]() 的把握认为“测评结果优秀与性别有关”
的把握认为“测评结果优秀与性别有关”
【解析】试题分析:(1)根据分层抽样抽样比相等,求出x,y的值,从表2中非优秀学生共5人,从这5人中任选2人的所有可能结果共10种,其中恰有1人测评等级为合格”的结果共6种,故所求概率为![]() .
.
(2)由1﹣0.9=0.1,p(k2>2.706)=0.10,计算K2=![]() =
=![]() =
=![]() =1.125<2.706,可得没有90%的把握认为“测评结果优秀与性别有关”.
=1.125<2.706,可得没有90%的把握认为“测评结果优秀与性别有关”.
试题解析:(1)设从高一年级男生中抽出m人,则![]() =
=![]() ,m=25,
,m=25,
∴x=25﹣20=5,y=20﹣18=2,
表2中非优秀学生共5人,记测评等级为合格的3人为a,b,c,尚待改进的2人为A,B,
则从这5人中任选2人的所有可能结果为:(a,b)(a,c)(b,c)(A,B)(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共10种.
设事件C表示“从表二的非优秀学生5人中随机选取2人,恰有1人测评等级为合格”,
则C的结果为:(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共6种.
∴P(C)=![]() =
=![]() ,故所求概率为
,故所求概率为![]() .
.
(2)∵1﹣0.9=0.1,p(k2>2.706)=0.10,
而K2=![]() =
=![]() =
=![]() =1.125<2.706,
=1.125<2.706,
所以没有90%的把握认为“测评结果优秀与性别有关”.

【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
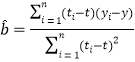 ,
,![]()