题目内容

已知等差数列{an}的首项a1=1，公差d＞0．且a2，a5，a14分别是等比数列{bn}的b1，b2，b3．
（Ⅰ）求数列{an}与{bn}的通项公式；
（Ⅱ）设数列{Cn}对任意自然数n均有
c1
b1
+
c2
b2
+…+
cn
bn
=an+1成立，求c1+c2+…+c2013的值．
（1）∵a2=1+d，a5=1+4d，a14=1+13d，且a2，a5，a14成等比数列，
∴（1+4d）2=（1+d）（1+13d），解得d=2，
∴an=1+（n-1）•2=2n-1，
又b1=a2=3，b2=a5=9，
∴q=3，bn=3•3n-1=3n；
（2）
c1
b1
+
c2
b2
+…+
cn
bn
=an+1，即
C1
3
+
C2
32
+…+
Cn
3n
=2n+1①，
则n≥2时，
C1
3
+
C2
32
+…+
Cn-1
3n-1
=2n-1②，
①-②得，
Cn
3n
=2，所以Cn=2•3n（n≥2），
n=1时，C1=9，
所以Cn=
2•3n，n≥2
9，n=1
，
所以c1+c2+…+c2013=9+2•32+2•33+…+2•32013
=9+2•
32(1-32012)
1-3
=32014；
练习册系列答案
相关题目
已知数列{an}的各项均为正数，观察程序框图，若k=5，k=10时，分别有S=
5
11
和S=
10
21

（1）试求数列{an}的通项；
（2）令bn=2an，求b1+b2+…+bm的值．
在等比数列{an}中，Sn为{an}的前n项和，且S3=
7
2
，S6=
63
2
，
（1）求an．
（2）求数列{nan}的前n项和Tn．
已知等差数列前三项为a，4，3a，前n项的和为sn，sk=2550．
（1）求a及k的值；
（2）求
1
s1
+
1
s2
+…+
1
sn
．
等差数列{an}中，a1=3，公差d=2，Sn为前n项和，求
1
S1
+
1
S2
+…+
1
Sn
．
已知数列{an}满足Sn=n2an（n∈N*），其中Sn是{an}的前n项和，且a1=1，求
（1）求an的表达式；
（2）求Sn．
已知无穷数列{an}的前n项和为Sn，且满足Sn=A
a2n
+Ban+C，其中A、B、C是常数．
（1）若A=0，B=3，C=-2，求数列{an}的通项公式；
（2）若A=1，B=
1
2
，C=
1
16
，且an＞0，求数列{an}的前n项和Sn；
（3）试探究A、B、C满足什么条件时，数列{an}是公比不为-1的等比数列．
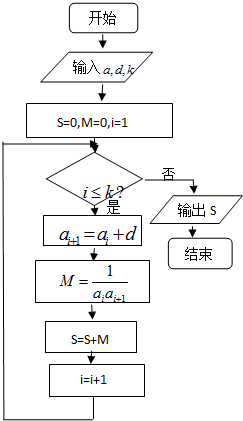
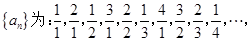已知数列依它的前10项的规律，则
         _.
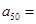记数列{an}的前n项和为Sn，且Sn=2（an-1），则a2=（　　）
A．4B．2C．1D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网