题目内容
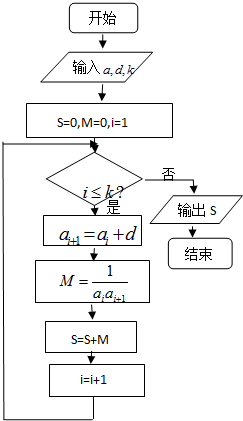
已知数列{an}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=
和S=
(1)试求数列{an}的通项;
(2)令bn=2an,求b1+b2+…+bm的值.
| 5 |
| 11 |
| 10 |
| 21 |
(1)试求数列{an}的通项;
(2)令bn=2an,求b1+b2+…+bm的值.

(1)由框图可知
S=
+
+…+
∵ai+1=ai+d,∴{an}是等差数列,设公差为d,则有
=
(
-
)
∴S=
(
-
+
-
+…+
-
)=
(
-
),
由题意可知,k=5时,S=
;k=10时,S=
∴
得
或
(舍去)
故an=a1+(n-1)d=2n-1
(2)由(1)可得:bn=2an=22n-1
∴b1+b2++bm=21+23++22m-1
=
=
(4m-1)
S=
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| akak+1 |
∵ai+1=ai+d,∴{an}是等差数列,设公差为d,则有
| 1 |
| akak+1 |
| 1 |
| d |
| 1 |
| ak |
| 1 |
| ak+1 |
∴S=
| 1 |
| d |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| ak |
| 1 |
| ak+1 |
| 1 |
| d |
| 1 |
| a1 |
| 1 |
| ak+1 |
由题意可知,k=5时,S=
| 5 |
| 11 |
| 10 |
| 21 |
∴
|
|
|
故an=a1+(n-1)d=2n-1
(2)由(1)可得:bn=2an=22n-1
∴b1+b2++bm=21+23++22m-1
=
| 2(1-4m) |
| 1-4 |
=
| 2 |
| 3 |

练习册系列答案
相关题目

 的值是 ( )
的值是 ( ) B
B  C
C  D
D 