题目内容
8．在△ABC中，sinA：sinC=3：4，∠B=120°，S△ABC=12$\sqrt{3}$，求a，b，c三边的边长．分析 利用正弦定理以及三角形的面积，然后利用余弦定理求出三角形的边长即可．
解答 解：在△ABC中，sinA：sinC=3：4，∠B=120°，S△ABC=12$\sqrt{3}$，
可得$\frac{a}{c}=\frac{3}{4}$，$\frac{1}{2}acsin120°=12\sqrt{3}$，
解得a=6，c=8．
有余弦定理可得b=$\sqrt{{a}^{2}{+c}^{2}-2accosB}$=$\sqrt{{6}^{2}{+8}^{2}-2×6×8cos120°}$=$\sqrt{148}$=$2\sqrt{37}$．
点评 本题考查三角形的解法，余弦定理的应用，考查计算能力．
练习册系列答案
相关题目
18．已知函数f（x）=tan（2x-$\frac{π}{3}$），则下列说法错误的是（ ）
| A． | 函数f（x）的周期为$\frac{π}{2}$ | |
| B． | 函数f（x）的值域为R | |
| C． | 点（$\frac{π}{6}$，0）是函数f（x）的图象一个对称中心 | |
| D． | f（$\frac{2π}{5}$）＜f（$\frac{3π}{5}$） |
16．
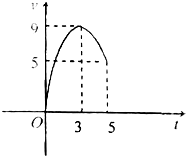某校举行玩具机器人竞速比赛，要求参赛的机器人在规定的轨道中前行5秒钟，以运动路程的长短来决定比赛成绩．已知某参赛玩具机器人的运动速度v（单位：米/秒）和时间t（单位：秒）满足的关系大致如图所示，那么该玩具机器人运动5秒钟后，行驶的路程s（单位：米）可以是（ ）
某校举行玩具机器人竞速比赛，要求参赛的机器人在规定的轨道中前行5秒钟，以运动路程的长短来决定比赛成绩．已知某参赛玩具机器人的运动速度v（单位：米/秒）和时间t（单位：秒）满足的关系大致如图所示，那么该玩具机器人运动5秒钟后，行驶的路程s（单位：米）可以是（ ）| A． | 25 | B． | $\frac{55}{2}$ | C． | $\frac{100}{3}$ | D． | 45 |
6．“序数”指每个数字比其左边的数字大的自然数（如1246），在两位的“序数”中任取一个数比36大的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{5}$ |