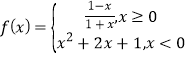Question

【题目】在平面直角坐标系xOy中，点，直线.

（1）求以点A为圆心，以为半径的圆与直线相交所得弦长；

（2）设圆的半径为1，圆心在上.若圆上存在点，使，求圆心的横坐标的取值范围.

Answer 1

【答案】（1）；（2）.

【解析】

（1）求得圆心到直线的距离，利用直线和圆相交所得弦长公式，求得弦长.

（2）设出圆的方程，设出点坐标，利用求得点的轨迹方程，根据圆和圆有公共点列不等式，解不等式求得的取值范围.

（1）设直线与圆A相交的弦为线段

则圆心到直线的距离.

由题意知，

解得.

（2）因为圆心在直线上，所以圆C的方程为.

设点，因为，

所以，化简得，即，

所以点M在以为圆心，2为半径的圆上.

由题意，点在圆C上，所以M是圆C与圆D的公共点，则， 所以

即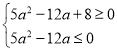

得

所以点C的横坐标的取值范围为.