题目内容
如图所示,在正方体ABCD—A1B1C1D1中,E、F、G、H分别是BC、CC1、C1D1、A1A的中点.求证:
(1)BF∥HD1;
(2)EG∥平面BB1D1D;
(3)平面BDF∥平面B1D1H.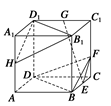
(1)BF∥HD1;
(2)EG∥平面BB1D1D;
(3)平面BDF∥平面B1D1H.

证明略
(1)如图所示,取BB1的中点M,易证四边形HMC1D1是平行四边形,∴HD1∥MC1.
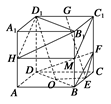
又∵MC1∥BF,∴BF∥HD1.
(2)取BD的中点O,连接EO,D1O,
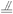 则OE
则OE 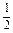 DC,
DC,
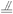
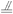 又D1G
又D1G 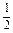 DC,∴OE? D1G,
DC,∴OE? D1G,
∴四边形OEGD1是平行四边形,
∴GE∥D1O.
又D1O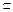 平面BB1D1D,∴EG∥平面BB1D1D.
平面BB1D1D,∴EG∥平面BB1D1D.
(3)由(1)知D1H∥BF,又BD∥B1D1,B1D1、HD1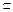 平面HB1D1,BF、BD
平面HB1D1,BF、BD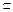 平面BDF,且B1D1∩HD1=D1,
平面BDF,且B1D1∩HD1=D1,
DB∩BF=B,∴平面BDF∥平面B1D1H.

又∵MC1∥BF,∴BF∥HD1.
(2)取BD的中点O,连接EO,D1O,
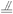 则OE
则OE 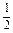 DC,
DC,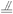
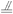 又D1G
又D1G 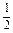 DC,∴OE? D1G,
DC,∴OE? D1G,∴四边形OEGD1是平行四边形,
∴GE∥D1O.
又D1O
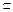 平面BB1D1D,∴EG∥平面BB1D1D.
平面BB1D1D,∴EG∥平面BB1D1D.(3)由(1)知D1H∥BF,又BD∥B1D1,B1D1、HD1
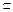 平面HB1D1,BF、BD
平面HB1D1,BF、BD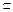 平面BDF,且B1D1∩HD1=D1,
平面BDF,且B1D1∩HD1=D1,DB∩BF=B,∴平面BDF∥平面B1D1H.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
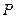 为
为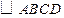 所在平面外一点,
所在平面外一点,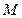 ,
,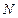 分别是
分别是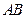 ,
,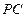 的中点,平面
的中点,平面 平面
平面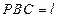 .
.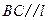 .
.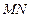 与平面
与平面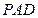 是否平行?试证明你的结论.
是否平行?试证明你的结论.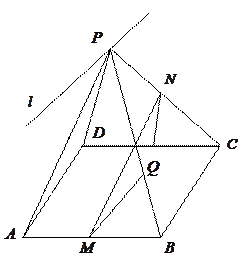

 ∶S△ABC.
∶S△ABC. 平面ABCD且直线FG∥直线A1B1.
平面ABCD且直线FG∥直线A1B1. ,
, 平面
平面 ,且
,且 ,
,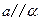 ,
,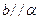 .
.
 中,
中, ,
, ,且
,且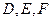 分别为
分别为 的中点.
的中点. ;
; 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?证明
?证明 你的结论.
你的结论.