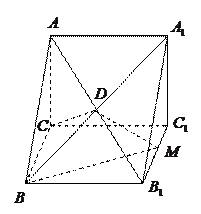题目内容
已知a、b、c是平面α内相交于一点O的三条直线,而直线l和α相交,并且和a、b、c三条直线成等角.
求证:l⊥α
求证:l⊥α
证法一:分别在a、b、c上取点A、B、C并使AO = BO = CO.设l经过O,在l上取一点P,在△POA、△POB、△POC中,
∵PO公用,AO = BO = CO,∠POA =∠POB=∠POC,
∴△POA≌△POB≌△POC
∴PA = PB = PC.取AB中点D.连结OD、PD,则OD⊥AB,PD⊥AB,
∵
∴ AB⊥平面POD
∵PO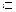 平面POD.
平面POD.
∴PO⊥AB.
同理可证 PO⊥BC
∵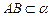 ,
, ,
,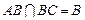
∴ PO⊥α,即l⊥α
若l不经过O时,可经过O作 ∥l.用上述方法证明
∥l.用上述方法证明 ⊥α,
⊥α,
∴l⊥α.
证法二:采用反证法
假设l不和α垂直,则l和α斜交于O.
同证法一,得到PA = PB = PC.
过P作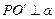 于
于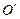 ,则
,则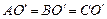 ,O是△ABC的外心.因为O也是△ABC的外心,这样,△ABC有两个外心,这是不可能的.
,O是△ABC的外心.因为O也是△ABC的外心,这样,△ABC有两个外心,这是不可能的.
∴假设l不和α垂直是不成立的.
∴l⊥α
若l不经过O点时,过O作 ∥l,用上述同样的方法可证
∥l,用上述同样的方法可证 ⊥α,
⊥α,
∴l⊥α
评述:(1)证明线面垂直时,一般都采用直接证法(如证法一),有时也采用反证法(如证法二)或同一法.
∵PO公用,AO = BO = CO,∠POA =∠POB=∠POC,
∴△POA≌△POB≌△POC
∴PA = PB = PC.取AB中点D.连结OD、PD,则OD⊥AB,PD⊥AB,
∵

∴ AB⊥平面POD
∵PO
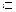 平面POD.
平面POD.∴PO⊥AB.
同理可证 PO⊥BC
∵
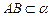 ,
, ,
,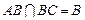
∴ PO⊥α,即l⊥α
若l不经过O时,可经过O作
 ∥l.用上述方法证明
∥l.用上述方法证明 ⊥α,
⊥α,∴l⊥α.
证法二:采用反证法
假设l不和α垂直,则l和α斜交于O.
同证法一,得到PA = PB = PC.
过P作
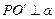 于
于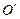 ,则
,则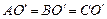 ,O是△ABC的外心.因为O也是△ABC的外心,这样,△ABC有两个外心,这是不可能的.
,O是△ABC的外心.因为O也是△ABC的外心,这样,△ABC有两个外心,这是不可能的.∴假设l不和α垂直是不成立的.
∴l⊥α
若l不经过O点时,过O作
 ∥l,用上述同样的方法可证
∥l,用上述同样的方法可证 ⊥α,
⊥α,∴l⊥α
评述:(1)证明线面垂直时,一般都采用直接证法(如证法一),有时也采用反证法(如证法二)或同一法.

练习册系列答案
相关题目
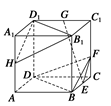
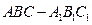 中,
中,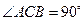 ,
,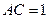 ,
,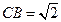 ,侧棱
,侧棱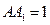 ,侧面
,侧面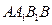 的两条对角线交点为
的两条对角线交点为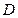 ,
,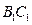 的中点为
的中点为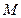 .
.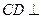 平面
平面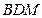 .
.