题目内容
3.已知△ABC的内角A,B,C所对的边分别为a,b,c,向量$\overrightarrow{m}$=(2sin$\frac{A}{2}$,cosA),$\overrightarrow{n}$=(1-2sin2$\frac{A}{4}$,-$\sqrt{15}$),且$\overrightarrow{m}$⊥$\overrightarrow{n}$(Ⅰ)求角A的余弦值;
(Ⅱ)若a=$\sqrt{6}$,求△ABC的面积最大值.
分析 (Ⅰ)根据向量数量积的定义,以及三角函数的关系式即可求角A的余弦值;
(Ⅱ)若a=$\sqrt{6}$,根据余弦定理求出bc的取值范围即可求△ABC的面积最大值.
解答 解:(Ⅰ)∵$\overrightarrow{m}$⊥$\overrightarrow{n}$,
∴$\overrightarrow{m}$•$\overrightarrow{n}$=2sin$\frac{A}{2}$(1-2sin2$\frac{A}{4}$)-$\sqrt{15}$cosA=0
即2sin$\frac{A}{2}$cos$\frac{A}{2}$=$\sqrt{15}$cosA,
即sinA=$\sqrt{15}$cosA,
在△ABC中,sinA>0,cosA>0,
解得cosA=$\frac{1}{4}$.
(Ⅱ)若a=$\sqrt{6}$,由余弦定理得a2=b2+c2-2bccosA,
又b2+c2≥2bc,
∴a2≥2bc-2bccosA,
即6≥2bc-$\frac{1}{4}$×2bc=$\frac{3}{2}$bc,
∴bc≤4,当且仅当b=c=2时取等号,
△ABC的面积S=$\frac{1}{2}bcsinA$=$\frac{1}{2}bc×\frac{\sqrt{15}}{4}=\frac{\sqrt{15}}{8}bc$$≤\frac{\sqrt{15}}{8}×4$=$\frac{\sqrt{15}}{2}$,
即三角形面积的最大值为$\frac{\sqrt{15}}{2}$.
点评 本题主要考查余弦定理和三角形的面积的计算,利用向量的数量积进行化简是解决本题的关键.考查学生的运算能力.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
13.已知p:x2-5x+6≤0,q:|x-a|<1,若p是q的充分不必要条件,则实数a的取值范围为( )
| A. | (-∞,3] | B. | [2,3] | C. | (2,+∞) | D. | (2,3) |
 如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.
如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.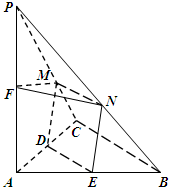 如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=2BC=PC=2,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN∥BC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=2BC=PC=2,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN∥BC. 如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.
如图,已知AB为半圆O的直径,C为圆弧上一点,过点C作半圆的切线CF,过点A作CF的垂线,垂足为D,AD交半圆于点E,连结EC,BC,AC.