题目内容
5.正数列{an}的前n项和Sn满足:rSn=anan+1-1,a1=a>0,常数r∈N.(Ⅰ)求证:an+2-an为定值;
(Ⅱ)若数列{an}是一个周期数列(即存在非零常数T,使an+T=an恒成立),求该数列的最小正周期;
(Ⅲ)若数列{an}是一个各项为有理数的等差数列,求Sn.
分析 (Ⅰ)由rSn=anan+1-1,a1=a>0,利用递推式可得ran+1=an+1(an+2-an),由于an+1>0,即可证明an+2-an为定值.
(Ⅱ)当n=1时,ra=aa2-1,${a}_{2}=r+\frac{1}{a}$,根据数列是隔项成等差,写出数列的前几项.当r>0时,奇数项和偶数项都是单调递增的,不可能是周期数列.当r=0时,写出数列的前几项.对a分类讨论:当a>0且a≠1时,与当a=1时,即可得出.
(Ⅲ)由数列{an}是一个有理数等差数列,可得a+a+r=2$(r+\frac{1}{a})$,解得a=$\frac{r+\sqrt{16+{r}^{2}}}{4}$是有理数.设r2+16=k2,r,k均是非负整数.对r分类讨论:r=0时,r≠0时,(k-r)(k+r)=16=4×4=2×8,可以分解成8组,即可得出.
解答 (Ⅰ)证明:∵rSn=anan+1-1,a1=a>0,rSn+1=an+1an+2-1,∴ran+1=an+1(an+2-an),∵an+1>0,
∴an+2-an=r为定值.
(Ⅱ)解:当n=1时,ra=aa2-1,∴${a}_{2}=r+\frac{1}{a}$,
根据数列是隔项成等差,写出数列的前几项:a,r+$\frac{1}{a}$,a+r,2r+$\frac{1}{a}$,a+2r,3r+$\frac{1}{a}$,….
当r>0时,奇数项和偶数项都是单调递增的,
∴不可能是周期数列,
当r=0时,写出数列的前几项:a,$\frac{1}{a}$,a,$\frac{1}{a}$,a,$\frac{1}{a}$,….
∴当a>0且a≠1时,该数列的周期是2,当a=1时,该数列的周期是1,
(Ⅲ)解:∵数列{an}是一个有理数等差数列,∴a+a+r=2$(r+\frac{1}{a})$,
化简2a2-ar-2=0,a=$\frac{r+\sqrt{16+{r}^{2}}}{4}$是有理数.设r2+16=k2,r,k均是非负整数,
r=0时,a=1,a1=1,Sn=n,
r≠0时,(k-r)(k+r)=16=4×4=2×8,
可以分解成8组,其中只有$\left\{\begin{array}{l}{r=3}\\{k=5}\end{array}\right.$,符合要求,此时a=2,an=$\frac{3n+1}{2}$,Sn=$\frac{n(3n+5)}{4}$.
点评 本题考查了等差数列的通项公式、周期数列、递推式的应用,考查了分类讨论思想方法、推理能力与计算能力,属于中档题.

| A. | 4 | B. | 4$\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
 如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.
如图,直线PQ与⊙O相切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连结CB,并延长与直线PQ相交于点Q,若AQ=6,AC=5.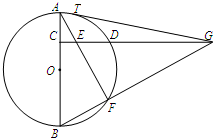 如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T.
如图,C是⊙O的直径AB上一点,CD⊥AB,与⊙O相交于点D,与弦AF交于点E,与BF的延长线交于点G,GT与⊙O相切于点T. 将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上.
将5个全等的正方形按如图所示方式放置在一个的矩形OEFG内,其中顶点P、C、Q、D分别在矩形的四条边上.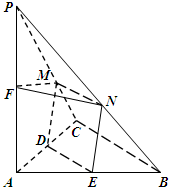 如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=2BC=PC=2,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN∥BC.
如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=2BC=PC=2,AC⊥BC,D、E、F分别为AC、AB、AP的中点,M、N分别为线段PC、PB上的动点,且有MN∥BC.