题目内容
17.下列命题:①常数列既是等差数列又是等比数列;
②若直线l:y=kx-$\sqrt{3}$与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是($\frac{π}{6}$,$\frac{π}{2}$);
③若α,β都是锐角,sinα=$\frac{4}{5}$,cos(α+β)=$\frac{5}{13}$,则cosβ=$\frac{63}{65}$
④如果(a-2)x2+(a-2)x-1≤0对任意实数x总成立,则a的取值范围是[-2,2].
其中所有正确命题的序号是②③④.
分析 根据等比数列的定义,可以判断①,
联立两直线方程到底一个二元一次方程组,求出方程组的解集即可得到交点的坐标,根据交点在第一象限得到横纵坐标都大于0,联立得到关于k的不等式组,求出不等式组的解集即可得到k的范围,然后根据直线的倾斜角的正切值等于斜率k,根据正切函数图象得到倾斜角的范围可判断②,
根据两角差的余弦公式,可得cosβ=cos(α+β-α)=$\frac{63}{65}$,故可判断③,
根据不等式恒成立的问题,分类讨论,即可判断④.
解答 解:对于①,例如,0,0,0,…,0是等差数列,不是等比数列,故①不正确,
对于②解:联立两直线方程得:$\left\{\begin{array}{l}{y=kx-\sqrt{3}}\\{2x+3y-6=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{3\sqrt{3}+6}{2+3k}}\\{y=\frac{6k-2\sqrt{3}}{2+3k}}\end{array}\right.$
因为两直线的交点在第一象限,所以得到$\left\{\begin{array}{l}{\frac{3\sqrt{3}+6}{2+3k}>0}\\{\frac{6k-2\sqrt{3}}{2+3k}>0}\end{array}\right.$,
解得:k>$\frac{\sqrt{3}}{3}$,
设直线l的倾斜角为θ,则tanθ>$\frac{\sqrt{3}}{3}$,所以θ∈($\frac{π}{6}$,$\frac{π}{2}$).故②正确;
对于③∵α,β都是锐角,sinα=$\frac{4}{5}$,cos(α+β)=$\frac{5}{13}$,∴cosα=$\frac{3}{5}$,sin(α+β)=$\frac{12}{13}$,
∴cosβ=cos(α+β-α)=cos(α+β)cosα+sin(α+β)sinα=$\frac{5}{13}×\frac{3}{5}$+$\frac{12}{13}×\frac{4}{5}$=$\frac{63}{65}$,故③正确;
对于④,当a=2时,-1≤0成立,当a≠2时,由题意得$\left\{\begin{array}{l}{a-2<0}\\{(a-2)^{2}+4(a-2)<0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a-2<0}\\{(a-2)^{2}+4(a-2)≤0}\end{array}\right.$,解得-2≤a<2,所以a的取值范围为[-2,2],故④正确,
故答案为:②③④.
点评 本题考查的知识点是命题的真假判断与应用,其中熟练掌握上述基本知识点,并应用这些基本知识点判断题目命题的真假是解答本题的关键.

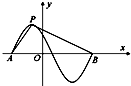 函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )
函数f(x)=cos(πx+φ)(φ>0)的图象如图所示,设P是图象的最高点,A、B是图象与x轴的交点,则tan∠APB=( )| A. | 10 | B. | 8 | C. | $\frac{8}{7}$ | D. | $\frac{4}{7}$ |
| A. | 向右平移$\frac{π}{12}$个单位 | B. | 向左平移$\frac{π}{12}$个单位 | ||
| C. | 向右平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
| A. | (-1,0) | B. | (-1,-2) | C. | (-1,2) | D. | (1,-2) |
 如图,已知A,B,C,D四点不共面,且AB∥平面α,CD∥平面α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,求证:EFHG是一个平行四边形.
如图,已知A,B,C,D四点不共面,且AB∥平面α,CD∥平面α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,求证:EFHG是一个平行四边形.