题目内容
12.已知函数f(x)=$\left\{\begin{array}{l}{sinπx,0<x<0.5}\\{ln(x+2),0.5<x<1}\\{f(x-1),x>1}\end{array}\right.$,e为自然对数的底数,且e≈2.718(Ⅰ)求$f(\frac{1}{4})$的值;
(Ⅱ)求f(e+1)的值.
分析 (Ⅰ)由已知中函数f(x)=$\left\{\begin{array}{l}{sinπx,0<x<0.5}\\{ln(x+2),0.5<x<1}\\{f(x-1),x>1}\end{array}\right.$,将x=$\frac{1}{4}$代入可得$f(\frac{1}{4})$的值;
(Ⅱ)由已知中函数f(x)=$\left\{\begin{array}{l}{sinπx,0<x<0.5}\\{ln(x+2),0.5<x<1}\\{f(x-1),x>1}\end{array}\right.$,e≈2.718,结合对数的运算性质,可得f(e+1)的值.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{sinπx,0<x<0.5}\\{ln(x+2),0.5<x<1}\\{f(x-1),x>1}\end{array}\right.$,
(Ⅰ)$f(\frac{1}{4})$=$sin\frac{π}{4}$=$\frac{\sqrt{2}}{2}$;
(Ⅱ)∵e≈2.718
∴e+1≈3.718
∴f(e+1)=f(e)=f(e-1)=f(e-2)=ln(e-2+2)=lne=1.
点评 本题考查的知识点是分段函数的应用,函数求值,是分段函数与对数运算的综合应用,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.若|x|≤1时都有|ax+b|≤1,则不等必成立的是( )
| A. | |a|≤|b|≤1 | B. | |b|≤|a|≤1 | C. | |a|≤1,|b|≤1 | D. | |a|+|b|≤1 |
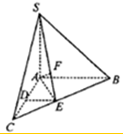 如图,在三棱锥S-ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D、E分别是AC、BC的中点,F在SE上,且SF=2FE
如图,在三棱锥S-ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D、E分别是AC、BC的中点,F在SE上,且SF=2FE