题目内容
【题目】如图,在半径为2,圆心角为 ![]() 的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧
的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧 ![]() 上,且OM=ON,MN∥PQ.
上,且OM=ON,MN∥PQ. 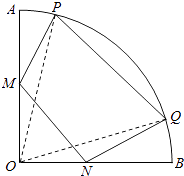
(1)若M、N分別是OA、OB中点,求四边形MNQP面积的最大值.
(2)PQ=2,求四边形MNQP面积的最大值.
【答案】
(1)解:连接OP,OQ,则四边形MNQP为梯形.
设∠AOP=∠BOQ=θ∈(0, ![]() ),则∠POQ=
),则∠POQ= ![]() ﹣2θ,且此时OM=ON=1,
﹣2θ,且此时OM=ON=1,
四边形MNQP面积S= ![]() sinθ+
sinθ+ ![]() sinθ+
sinθ+ ![]() ×2sin(
×2sin( ![]() ﹣2θ)﹣
﹣2θ)﹣ ![]() =﹣4sin2θ+2sinθ+
=﹣4sin2θ+2sinθ+ ![]() ,
,
∴sinθ= ![]() ,S取最大值
,S取最大值 ![]()
(2)解:设OM=ON=x∈(0,2),
由PQ=2可知∠POQ= ![]() ,∠AOQ=∠BOP=
,∠AOQ=∠BOP= ![]() ,
,
∴sin ![]() =
= ![]() ,
,
∴四边形MNQP面积S= ![]() x+
x+ ![]() x+
x+ ![]() ﹣
﹣ ![]() x2=﹣
x2=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
∴x= ![]() ,S取最大值为
,S取最大值为 ![]()
【解析】(1)设∠AOP=∠BOQ=θ∈(0, ![]() ),则∠POQ=
),则∠POQ= ![]() ﹣2θ,且此时OM=ON=1,利用分割法,即可求四边形MNQP面积的最大值.(2)PQ=2,可知∠POQ=
﹣2θ,且此时OM=ON=1,利用分割法,即可求四边形MNQP面积的最大值.(2)PQ=2,可知∠POQ= ![]() ,∠AOQ=∠BOP=
,∠AOQ=∠BOP= ![]() ,利用分割法,即可求四边形MNQP面积的最大值.
,利用分割法,即可求四边形MNQP面积的最大值.
【考点精析】本题主要考查了三角函数的最值的相关知识点,需要掌握函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目