题目内容
【题目】设{an}是各项都为正数的等比数列,{bn}是等差数列,且a1=b1=1,a3+b5=13,a5+b3=21.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn , 求数列{Snbn}的前n项和Tn .
【答案】解:(Ⅰ)设各项都为正数的等比数列{an}的公比是q,且q>0,等差数列{bn}的公差是d,
∵a1=b1=1,a3+b5=13,a5+b3=21,
∴ 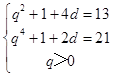 ,即
,即 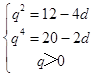 ,
,
整理,得2q4﹣q2﹣28=0,q>0
解得d=2,q=2,
∴an=2n﹣1 , bn=1+(n﹣1)d=2n﹣1.
(Ⅱ)∵{an}是首项为1,公比为2的等比数列,
∴Sn= ![]() =2n﹣1,
=2n﹣1,
∵bn=2n﹣1,
∴Snbn=(2n﹣1)(2n﹣1)=(2n﹣1)2n﹣2n+1,
∴Tn=[1×2+3×22+5×23+…+(2n﹣1)2n]﹣2(1+2+3+…+n)+n,
设S=1×2+3×22+5×23+…+(2n﹣1)2n , ①
则2S=1×22+3×23+5×24+…+(2n﹣1)×2n+1 , ②
①﹣②,得:
﹣S=2+22+23+…+2n﹣(2n﹣1)2n+1
= ![]() ﹣(2n﹣1)2n+1
﹣(2n﹣1)2n+1
=2n+1﹣2﹣(2n﹣1)2n+1 ,
∴S=2+(n+1)2n+2 ,
∴Tn=[1×2+3×22+5×23+…+(2n﹣1)2n]﹣2(1+2+3+…+n)+n
=2+(n+1)2n+2﹣2× ![]() +n
+n
=(n+1)2n+2﹣n2+2.
【解析】(Ⅰ)由已知条件,利用等差数列和等比数列的通项公式建立方程组,求出公差和公比,由此能求出数列{an},{bn}的通项公式.(Ⅱ)先求出数列{an}的前n项和Sn , 再求出Snbn的表达式,然后利用分组求和法、错位相减法和等等数列前n项和公式能求出Tn .
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系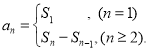 才能正确解答此题.
才能正确解答此题.

 小夫子全能检测系列答案
小夫子全能检测系列答案