题目内容
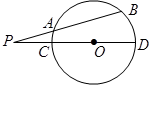
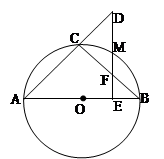
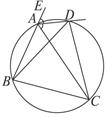
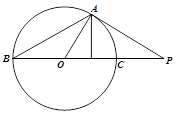
如图,BA是圆O的直径,延长BA至E,使得AE=AO,过E点作圆O的割线交圆O于D、E,使AD=DC,

求证: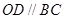 ;
;
若ED=2,求圆O的内接四边形ABCD的周长。

求证:
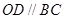 ;
;若ED=2,求圆O的内接四边形ABCD的周长。
证明:连接AC,因为OD为圆O的半径,AD=DC,所以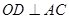 ,故
,故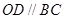 。
。
周长为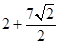
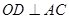 ,故
,故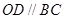 。
。周长为
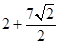
试题分析:(1)证明:连接AC,因为OD为圆O的半径,AD=DC,所以
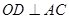 ,故
,故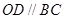 。
。(2)周长为AD+CD+BC+BA=
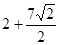 .
.点评:证明主要依据平面几何中的直线线段间的性质完成,此类题目难度不大

练习册系列答案
相关题目
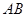 是圆
是圆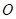 的直径,
的直径,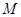 为圆上一点,
为圆上一点,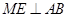 ,垂足为
,垂足为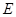 ,点
,点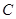 为圆
为圆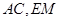 交于点
交于点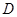 ,
,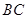 交
交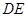 于点
于点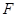 .
.
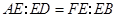 ;(2)
;(2)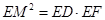 .
.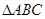 的面积为1,点
的面积为1,点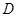 在
在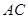 上,
上,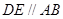 ,连结
,连结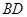 ,设
,设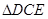 、
、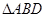 、
、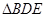 中面积最大者的值为
中面积最大者的值为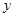 ,则
,则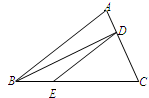
 ,则
,则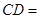

 为锐角△
为锐角△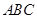 的内心,且
的内心,且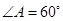 ,点
,点 为内切圆
为内切圆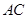 的切点,过点
的切点,过点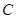 作直线
作直线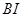 的垂线,垂足为
的垂线,垂足为 .
.
 ;
; 的值.
的值.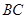 是半径为
是半径为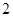 的圆
的圆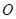 的直径,点
的直径,点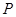 在
在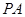 是圆
是圆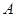 在直径
在直径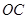 的中点,则
的中点,则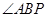 =
= 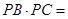 .
.
 AB于点D,则CD= 。
AB于点D,则CD= 。
 的割线
的割线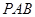 交圆
交圆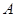 、
、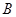 两点,割线
两点,割线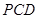 经过圆心.已知
经过圆心.已知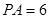 ,
,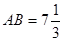 ,
,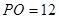 .则圆
.则圆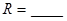 .
.