题目内容
已知函数 (
( ).
).
(1)证明:当 时,
时, 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时 的单调区间;
的单调区间;
(2)已知函数 ,函数
,函数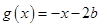 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)证明详见解析, 在
在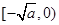 是减函数,在
是减函数,在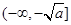 是增函数;(2)
是增函数;(2)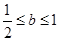 .
.
解析试题分析:(1)根据函数单调性的定义进行证明即①设 ;②作差:
;②作差: ;③因式分解到最简
;③因式分解到最简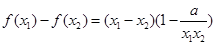 ;④根据条件判定符号;⑤作出结论,经过这五步即可证明
;④根据条件判定符号;⑤作出结论,经过这五步即可证明 在
在 单调递减,同理可证
单调递减,同理可证 在
在 是增函数,最后由奇函数的性质得出;
是增函数,最后由奇函数的性质得出; 在
在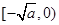 是减函数,在
是减函数,在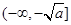 是增函数;(2)先将“对任意
是增函数;(2)先将“对任意 ,总存在
,总存在 ,使得
,使得 成立”转化为“函数
成立”转化为“函数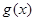 在区间
在区间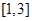 的值域包含了
的值域包含了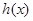 在区间
在区间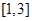 的值域”,分别根据函数的单调性求出这两个函数的值域,最后由集合的包含关系即可得到
的值域”,分别根据函数的单调性求出这两个函数的值域,最后由集合的包含关系即可得到 的取值范围.
的取值范围.
试题解析:(1)证明:当 时
时
①设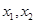 是区间
是区间 上的任意两个实数,且
上的任意两个实数,且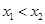 ,则
,则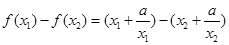
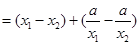
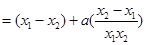
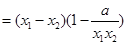
∵ ,∴
,∴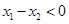 ,
,
∴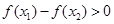 ,即
,即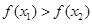
∴ 在
在 是减函数 4分
是减函数 4分
②同理可证 在
在 是增函数 5分
是增函数 5分
综上所述得:当 时,
时,  在
在 是减函数,在
是减函数,在 是增函数 6分
是增函数 6分
∵函数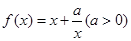 是奇函数,根据奇函数图像的性质可得
是奇函数,根据奇函数图像的性质可得
当 时,
时, 在
在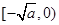 是减函数,在
是减函数,在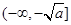 是增函数 8分
是增函数 8分
(2)∵ 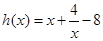 (
(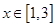 ) 8分
) 8分
由(1)知: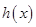 在
在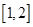 单调递减,
单调递减, 单调递增
单调递增
∴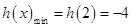
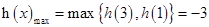 ,
,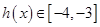 10分
10分
又∵ 在
在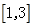 单调递减
单调递减
∴由题意知: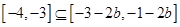
于是有: ,解得
,解得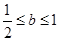 12分.
12分.
考点:1.函数的单调性与最值;2.函数的奇偶性;3.函数的值域.

练习册系列答案
相关题目
 .
. 的单调区间;
的单调区间; ,求函数
,求函数 .
. 的不等式
的不等式 ;
; 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. ,
, .
. ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明; 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围; 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1. 的图象过点(2,0).
的图象过点(2,0).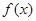 的奇偶性;
的奇偶性; 上的单调性,并给予证明;
上的单调性,并给予证明;