题目内容
已知函数
(1)求 的定义域;
的定义域;
(2)当 为何值时,函数值大于1.
为何值时,函数值大于1.
(1)当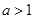 时,定义域为
时,定义域为 ,当
,当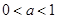 时,定义域为
时,定义域为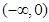 ;(2)当
;(2)当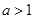 时,
时,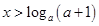 时,函数值大于1;当
时,函数值大于1;当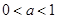 时,
时, 时,函数值大于1.
时,函数值大于1.
解析试题分析:(1)首先根据对数的真数大于0,然后分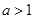 与
与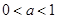 两种情况求函数的定义域;(2)由不等式
两种情况求函数的定义域;(2)由不等式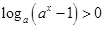 分
分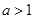 与
与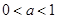 两种情况进行求解.
两种情况进行求解.
试题解析:(1)由已知,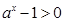 ,即
,即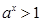 ,
,
当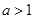 时,
时,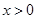 ,当
,当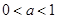 时,
时,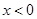 ,
,
∴当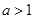 时,定义域为
时,定义域为 ,当
,当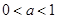 时,定义域为
时,定义域为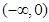 .
.
(2)当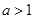 时,由
时,由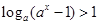 得
得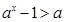 ,即
,即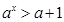 ,∴
,∴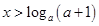 ,
,
当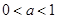 时,由
时,由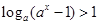 得
得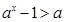 ,即
,即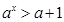 ,∴
,∴ ,
,
∴当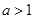 时,
时,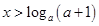 时,函数值大于1;当
时,函数值大于1;当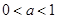 时,
时, 时,函数值大于1.
时,函数值大于1.
考点:1.函数的定义域;2.对数函数的单调性;3.不等式的解法.

练习册系列答案
相关题目
 ,满足
,满足 .
. 的不等式
的不等式 .
. (
( ).
). 时,
时, 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时 ,函数
,函数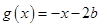 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.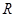 的函数
的函数
 的图象,并指出
的图象,并指出 有两个解,求出
有两个解,求出 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明). 为奇函数,且当
为奇函数,且当 时,
时, 求
求
 (其中
(其中 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为 元/件.
元/件. .
. ,求实数x的取值范围;
,求实数x的取值范围; 的最大值.
的最大值.
 的定义域和值域;(2)若函数
的定义域和值域;(2)若函数 ,求
,求 的值。
的值。 ,两个函数
,两个函数 ,
,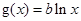 的图像关于直线
的图像关于直线 对称.
对称. 满足的关系式;
满足的关系式; 取何值时,函数
取何值时,函数 有且只有一个零点;
有且只有一个零点; 时,在
时,在 上解不等式
上解不等式 .
.