题目内容
已知函数 ,
, .
.
(1)若 ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若存在实数 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
(1)奇函数,(2) ,(3)
,(3) 
解析试题分析:(1)函数奇偶性的判定,一要判定定义域是否关于原点对称,二要判定 与
与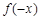 是否相等或相反,(2)函数
是否相等或相反,(2)函数 是分段函数,每一段都是二次函数的一部分,因此研究
是分段函数,每一段都是二次函数的一部分,因此研究 单调性,必须研究它们的对称轴,从图像可观察得到实数
单调性,必须研究它们的对称轴,从图像可观察得到实数 满足的条件:
满足的条件: ,(3)研究方程根的个数,通常从图像上研究,结合(2)可研究出函数
,(3)研究方程根的个数,通常从图像上研究,结合(2)可研究出函数 图像.分三种情况研究,一是
图像.分三种情况研究,一是 上单调增函数,二是先在
上单调增函数,二是先在 上单调增,后在
上单调增,后在 上单调减,再在
上单调减,再在 上单调增,三是先在
上单调增,三是先在 上单调增,后在
上单调增,后在 上单调减,再在
上单调减,再在 上单调增.
上单调增.
试题解析:(1)函数 为奇函数.[来
为奇函数.[来
当 时,
时, ,
, ,∴
,∴
∴函数 为奇函数; 3分
为奇函数; 3分
(2) ,当
,当 时,
时, 的对称轴为:
的对称轴为: ;
;
当 时,
时, 的对称轴为:
的对称轴为: ;∴当
;∴当 时,
时, 在R上是增函数,即
在R上是增函数,即 时,函数
时,函数 在
在 上是增函数; 7分
上是增函数; 7分
(3)方程 的解即为方程
的解即为方程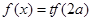 的解.
的解.
①当 时,函数
时,函数 在
在 上是增函数,∴关于
上是增函数,∴关于 的方程
的方程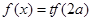 不可能有三个不相等的实数根; 9分
不可能有三个不相等的实数根; 9分
②当 时,即
时,即 ,∴
,∴ 在
在 上单调增,在
上单调增,在 上单调减,在
上单调减,在 上单调增,∴当
上单调增,∴当 时,关于
时,关于 的方程
的方程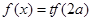 有三个不相等的实数根;即
有三个不相等的实数根;即 ,∵
,∵ ∴
∴ .
.
设 ,∵存在
,∵存在 使得关于
使得关于 的方程
的方程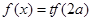 有三个不相等的实数根, ∴
有三个不相等的实数根, ∴ ,又可证
,又可证 在
在 上单调增
上单调增
∴ ∴
∴ ; 12分
; 12分
③当 时,即
时,即 ,∴
,∴

练习册系列答案
相关题目
 .
. 的定义域为集合B,若AÍB,求实数a的取值范围.
的定义域为集合B,若AÍB,求实数a的取值范围. (
( ).
). 时,
时, 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时 ,函数
,函数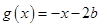 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 称为函数
称为函数 ,
, .
.  为奇函数,求实数
为奇函数,求实数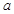 的值;
的值; 上的所有上界构成的集合;
上的所有上界构成的集合; 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数
 是偶函数.
是偶函数. 的值;
的值; ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数 的取值范围.
的取值范围.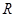 的函数
的函数
 的图象,并指出
的图象,并指出 有两个解,求出
有两个解,求出 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明). 为奇函数,且当
为奇函数,且当 时,
时, 求
求
 .
. ,求实数x的取值范围;
,求实数x的取值范围; 的最大值.
的最大值. .
.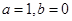 时,判断
时,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,若
时,若 ,求
,求 的值;
的值; ,且对任何
,且对任何 不等式
不等式 恒成立,求实数
恒成立,求实数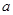 的取值范围.
的取值范围. 是奇函数,求a+b的值;
是奇函数,求a+b的值;