Question

17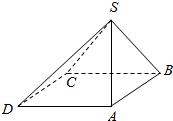．如图，四棱锥S-ABCD中，底面ABCD为菱形，侧面SBC⊥底面ABCD，已知∠ABC=60°，AB=SB=SC=2．
（1）证明：BC⊥SA；
（2）求直线SD与平面SAB所成角的正弦值．

Answer 1

分析 （1）设E点为BC的中点，连接SE、AE、AC，由已知得AE⊥BC，SE⊥BC，由此能证明BC⊥面SAE，从而得到BC⊥SA．
（2）以E为原点，EA为x轴，EB为y轴，ES为z轴，建立空间直角坐标系，由此利用向量法能求出直线SD与平面SAB所成角的正弦值．

解答 （1）证明：设E点为BC的中点，连接SE、AE、AC，
∵四棱锥S-ABCD中，底面ABCD为菱形，侧面SBC⊥底面ABCD，∠ABC=60°，AB=SB=SC=2．
∴△ABC为正三角形，△SBC也为正三角形，
∴AE⊥BC，SE⊥BC，
∵AE∩SE=E，∴BC⊥面SAE，
∵SA?平面SAE，∴BC⊥SA．
（2）解：以E为原点，EA为x轴，EB为y轴，ES为z轴，建立空间直角坐标系，
由已知得A（$\sqrt{3}$，0，0），B（0，1，0），S（0，0，$\sqrt{3}$），D（$\sqrt{3}$，-2，0），
$\overrightarrow{SD}$=（$\sqrt{3}$，-2，-$\sqrt{3}$），$\overrightarrow{SA}$=（$\sqrt{3}，0，-\sqrt{3}$），$\overrightarrow{SB}$=（0，1，-$\sqrt{3}$），
设平面SAB的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{SA}=\sqrt{3}x-\sqrt{3}z=0}\\{\overrightarrow{n}•\overrightarrow{SB}=y-\sqrt{3}z=0}\end{array}\right.$，取x=1，得$\overrightarrow{n}$=（1，$\sqrt{3}$，1），
设直线SD与平面SAB所成角为θ，
sinθ=|cos＜$\overrightarrow{SD}，\overrightarrow{n}$＞|=|$\frac{\overrightarrow{SD}•\overrightarrow{n}}{|\overrightarrow{SD}|•|\overrightarrow{n}|}$|=|$\frac{\sqrt{3}-2\sqrt{3}-\sqrt{3}}{\sqrt{10}•\sqrt{5}}$|=$\frac{\sqrt{6}}{5}$．
∴直线SD与平面SAB所成角的正弦值为$\frac{\sqrt{6}}{5}$．

点评 本题考查异面直线垂直的证明，考查线面角的正弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．