题目内容
2.已知△ABC中,角A、B、C所对的边分别为a、b、c,满足$\frac{b-a}{c}=\frac{sinB-sinC}{sinB+sinA}$.(1)求角A的值;
(2)若a,c,b成等差数列,试判断△ABC的形状.
分析 (1)由正弦定理化简已知等式可得$\frac{b-a}{c}=\frac{b-c}{b+a}$,整理由余弦定理得cosA的值,结合A是内角,即可求A的值.
(2)由题意可得2c=a+b,由(1)可知,a2=b2+c2-bc,可得(2c-b)2=b2+c2-bc,整理得:3c2-3bc=0,解得:a=b=c,从而得解.
解答 解:(1)由正弦定理,得:$\frac{b-a}{c}=\frac{b-c}{b+a}$,
整理,得:a2=b2+c2-bc,…(4分)
由余弦定理,得:$cosA=\frac{1}{2}$,
∵A是△ABC的内角,
∴$A=\frac{π}{3}$; …(7分)
(2)∵a,c,b成等差数列,
∴2c=a+b,
由(1)可知,a2=b2+c2-bc,
∴(2c-b)2=b2+c2-bc,整理,得:3c2-3bc=0,…(12分)
由c>0,得b=c,
∴a=b=c,
∴△ABC是等边三角形.…(14分)
(注:本题第二小问可以用角的化简来处理)
点评 本题主要考查了正弦定理,余弦定理,等差数列的性质的综合应用,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知f(x)是定义在R上且以4为周期的奇函数,当x∈(0,2)时,$f(x)={2^{|x-1|}}-\frac{3}{2}$,则函数f(x)在区间[0,8]上的所有零点的和为( )
| A. | 16 | B. | 32 | C. | 48 | D. | 52 |
14.函数y=f(x)在[-2,2]上的图象如图所示,则此函数的最小值、最大值分别是( )
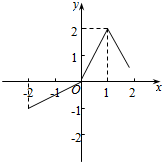
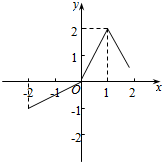
| A. | f(-2),0 | B. | 0,2 | C. | f(-2),2 | D. | f(2),2 |
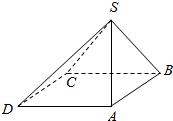 如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.
如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.