题目内容
7.已知F1,F2分别是离心率为$\frac{3}{5}$的椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,P为椭圆E上一点,且△F1F2P的周长为16.(1)求椭圆E的方程;
(2)若|PF1|=$\frac{16}{5}$,求点P到椭圆左顶点A的距离.
分析 (1)由椭圆的定义和离心率公式,解得a=5,c=3,b=4,进而得到椭圆方程;
(2)运用椭圆的第二定义,求得P的坐标,再由两点的距离公式计算即可得到.
解答 解:(1)△F1F2P的周长为16,
即有|PF1|+|PF2|+|F1F2|=2a+2c=16,
即a+c=8,
由e=$\frac{c}{a}$=$\frac{3}{5}$,
解得a=5,c=3,b=4,
则椭圆方程为$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1;
(2)椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左准线方程为x=-$\frac{25}{3}$,
由|PF1|=$\frac{16}{5}$,可得e=$\frac{|P{F}_{1}|}{d}$=$\frac{3}{5}$,
则d=xP+$\frac{25}{3}$=$\frac{16}{3}$,
即有xP=-3,yP=±$\frac{16}{5}$.
则点P到椭圆左顶点A(-5,0)的距离为:
$\sqrt{(-3+5)^{2}+(\frac{16}{5})^{2}}$=$\frac{2\sqrt{89}}{5}$.
点评 本题考查椭圆的定义、方程和性质,考查两点的距离公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
17.已知直线x-y-2=0与曲线x2-y2=4m的交点P在圆(x-4)2+y2=4的内部,则实数m的取值范围是( )
| A. | -1<m<3 | B. | -3<m<-1 | C. | 1<m<3 | D. | 2<m<3 |
19.若直线x+ay+6=0与直线(a-2)x+3y+2a=0平行,则a=( )
| A. | a=-1 | B. | a=3 | C. | a=3或a=-1 | D. | a=3且a=-1 |
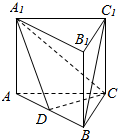 如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.
如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.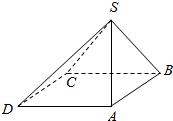 如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.
如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.