题目内容
5.已知方程$\frac{{x}^{2}}{4-m}-\frac{{y}^{2}}{2+m}=1$.(1)若方程表示双曲线,求实数m的取值范围.
(2)若方程表示椭圆,且椭圆的离心率为$\frac{\sqrt{3}}{2}$,求实数m的值.
分析 (1)方程表示双曲线,即有(4-m)(2+m)>0,解不等式即可得到所求范围;
(2)讨论焦点的位置,运用椭圆的a,b,c的关系和离心率公式,计算即可得到m的值.
解答 解:(1)方程表示双曲线,即有
(4-m)(2+m)>0,解得-2<m<4,
即m的取值范围是(-2,4);
(2)方程表示椭圆,
若焦点在x轴上,即有4-m>-2-m>0,
且a2=4-m,b2=-2-m,c2=a2-b2=6,
即有e2=$\frac{3}{4}$=$\frac{6}{4-m}$,解得m=-4;
若焦点在y轴上,即有0<4-m<-2-m,
且b2=4-m,a2=-2-m,c2=a2-b2=-6,不成立.
综上可得m=-4.
点评 本题考查椭圆、双曲线的方程和性质,注意它们的标准方程的区别,考查离心率公式的运用,属于基础题和易错题.

练习册系列答案
相关题目
20.已知△ABC是个一直角三角形,则经过平行投影后所得三角形是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 以上都有可能 |
14.函数y=f(x)在[-2,2]上的图象如图所示,则此函数的最小值、最大值分别是( )
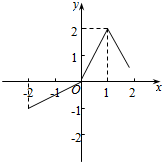
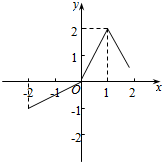
| A. | f(-2),0 | B. | 0,2 | C. | f(-2),2 | D. | f(2),2 |
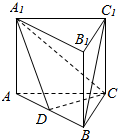 如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.
如图,在三棱柱A1B1C1中,四边形ABB1A1和ACC1A1都为矩形.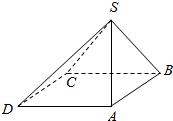 如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.
如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.