题目内容
已知a、b、c成等差数列,则直线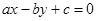 被曲线
被曲线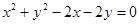 截得的弦长的最小值为
截得的弦长的最小值为
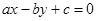 被曲线
被曲线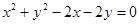 截得的弦长的最小值为
截得的弦长的最小值为A. | B. | C. | D.2 |
D
分析:利用等差数列的定义得到2b=a+c,求出圆心坐标及半径,求出圆心到直线的距离d,利用勾股定理求出弦长,求出最小值.
解:因为a,b,c成等差数列,
所以2b=a+c.
因为x2+y2-2x-2y=0表示以(1,1)为圆心,以
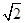 为半径的圆,
为半径的圆,则圆心到直线的距离为d=
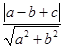 =
=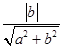 ,
,则直线ax-by+c=0被曲线x2+y2-2x-2y=0截得的弦长,
l=2
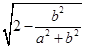 =2
=2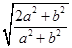 ≥2,
≥2,当且仅当a=0,且b≠0时,取等号.
所以0截得的弦长的最小值为2,
故选D.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
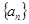 ,
,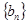 ,满足
,满足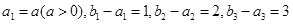 .
.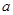 =1,求数列
=1,求数列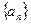 中,
中,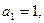 且点
且点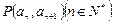 在直线
在直线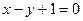 上.
上.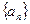 的通项公式;
的通项公式;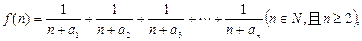 求函数
求函数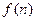 的最小值;
的最小值;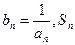 表示数列
表示数列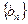 的前n项和.试问:是否存在关于
的前n项和.试问:是否存在关于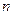 的整式
的整式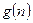 ,使得
,使得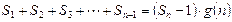 对于一切不小于2的自然数
对于一切不小于2的自然数 满足
满足 +
+ =4n-3(n∈
=4n-3(n∈ ).
). 的值;
的值; ;
; ≥5成立,求
≥5成立,求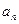 },其前n项和Sn满足Sn+1=2
},其前n项和Sn满足Sn+1=2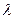 Sn+1(
Sn+1( 中,公比
中,公比 若
若 则
则 有( )
有( )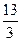 。
。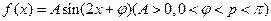 在
在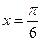 处取得最大值,且最大值为a3,求函数f(x)的解析式。
处取得最大值,且最大值为a3,求函数f(x)的解析式。 ,从中取出1
,从中取出1 ,再用水加满;然后再取出1
,再用水加满;然后再取出1 通项公式是
通项公式是 ,
, 是数列
是数列 项和,则
项和,则 等于( )
等于( )


