题目内容
(本题满分14分)已知数列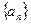 中,
中,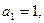 且点
且点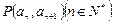 在直线
在直线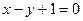 上.
上.
(1)求数列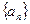 的通项公式;
的通项公式;
(2)若函数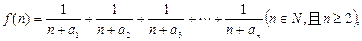 求函数
求函数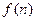 的最小值;
的最小值;
(3)设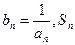 表示数列
表示数列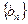 的前n项和.试问:是否存在关于
的前n项和.试问:是否存在关于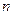 的整式
的整式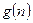 ,使得
,使得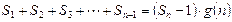 对于一切不小于2的自然数
对于一切不小于2的自然数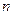 恒成立? 若存在,写出
恒成立? 若存在,写出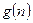 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
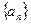 中,
中,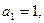 且点
且点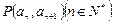 在直线
在直线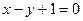 上.
上.(1)求数列
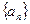 的通项公式;
的通项公式;(2)若函数
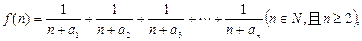 求函数
求函数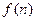 的最小值;
的最小值;(3)设
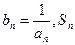 表示数列
表示数列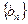 的前n项和.试问:是否存在关于
的前n项和.试问:是否存在关于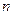 的整式
的整式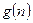 ,使得
,使得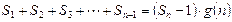 对于一切不小于2的自然数
对于一切不小于2的自然数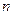 恒成立? 若存在,写出
恒成立? 若存在,写出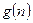 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.(1) ;(2)
;(2) ;(3)存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.
;(3)存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.
 ;(2)
;(2) ;(3)存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.
;(3)存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.解:(1)由点P 在直线
在直线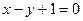 上,即
上,即 , ------2分
, ------2分
且 ,数列{
,数列{ }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
 ,
, 同样满足,所以
同样满足,所以 ------------4分
------------4分
(2)


所以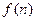 是单调递增,故
是单调递增,故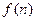 的最小值是
的最小值是 ----------------------8分
----------------------8分
(3) ,可得
,可得 ,
, -------10分
-------10分
 ,
, ……
……
以上各式相加,得:

 ,n≥2------------------12分
,n≥2------------------12分
 .
.
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.----14分
 在直线
在直线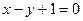 上,即
上,即 , ------2分
, ------2分且
 ,数列{
,数列{ }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列 ,
, 同样满足,所以
同样满足,所以 ------------4分
------------4分(2)



所以
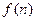 是单调递增,故
是单调递增,故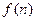 的最小值是
的最小值是 ----------------------8分
----------------------8分(3)
 ,可得
,可得 ,
, -------10分
-------10分 ,
, ……
……
以上各式相加,得:

 ,n≥2------------------12分
,n≥2------------------12分 .
.故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.----14分

练习册系列答案
相关题目
 满足
满足
 ,记
,记 ,证明:
,证明: 。
。
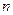 个等式为
个等式为 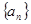 各项均为正数,如图给出程序框图,当
各项均为正数,如图给出程序框图,当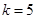 时,输出的
时,输出的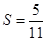 ,则数列
,则数列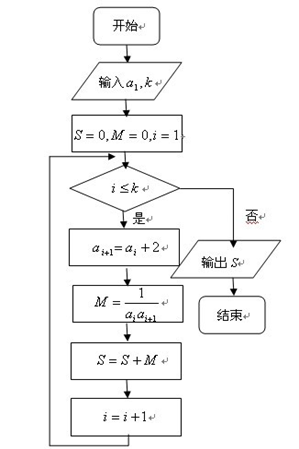




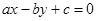 被曲线
被曲线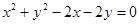 截得的弦长的最小值为
截得的弦长的最小值为


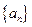 满足
满足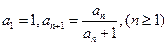 ,数列
,数列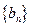 满足
满足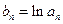 ,数列
,数列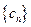
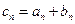 .
.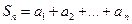 ,
,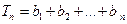 ,试比较
,试比较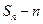 与
与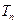 的大小,并证明;
的大小,并证明;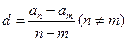 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列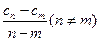 不是一个常数,但
不是一个常数,但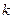 呢,若会,请求出
呢,若会,请求出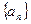 是等差数列,前n项和为Sn,
是等差数列,前n项和为Sn,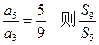 =
=  。
。