题目内容
(本小题满分12分)
已知数列{
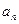 },其前n项和Sn满足Sn+1=2
},其前n项和Sn满足Sn+1=2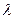 Sn+1(
Sn+1(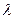 是大于0的常数),且a1=1,a3=4.
是大于0的常数),且a1=1,a3=4.(Ⅰ)求
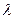 的值;
的值;(Ⅱ)求数列{an}的通项公式
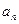 ;
;.解:(Ⅰ)由Sn+1=2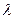 Sn+1得
Sn+1得
 ………………2分
………………2分
∴ ……………………………………6分
……………………………………6分
(Ⅱ)由Sn+1=2Sn+1整理得Sn+1+1=2(Sn+1),
∴数列{Sn+1}是以S1+1=2为首项,以2为公比的等比数列,……………………8分
∴Sn+1=2·2n-1,∴Sn=2n-1,
∴an=Sn-Sn-1=2n-1(n≥2)
∵当n=1时,a1=1满足an =2n-1,∴an =2n-1…………………………………………12分
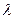 Sn+1得
Sn+1得 ………………2分
………………2分∴
 ……………………………………6分
……………………………………6分(Ⅱ)由Sn+1=2Sn+1整理得Sn+1+1=2(Sn+1),
∴数列{Sn+1}是以S1+1=2为首项,以2为公比的等比数列,……………………8分
∴Sn+1=2·2n-1,∴Sn=2n-1,
∴an=Sn-Sn-1=2n-1(n≥2)
∵当n=1时,a1=1满足an =2n-1,∴an =2n-1…………………………………………12分
略

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
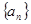 各项均为正数,如图给出程序框图,当
各项均为正数,如图给出程序框图,当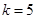 时,输出的
时,输出的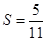 ,则数列
,则数列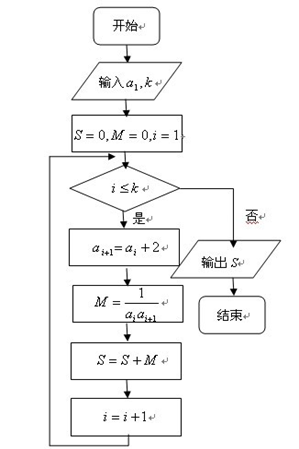




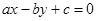 被曲线
被曲线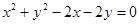 截得的弦长的最小值为
截得的弦长的最小值为


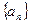 的各项均为正数,
的各项均为正数,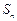 为其前
为其前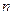 项和,对于任意
项和,对于任意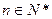 ,总有
,总有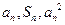 成等差数列.
成等差数列.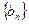 的前
的前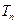 ,且
,且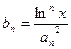 ,求证:对任意实数
,求证:对任意实数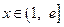 (
(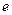 是常数,
是常数,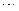 )和任意正整数
)和任意正整数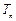
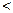 2;
2;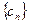 中,
中,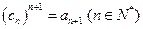 .,求数列
.,求数列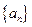 满足
满足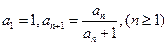 ,数列
,数列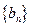 满足
满足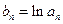 ,数列
,数列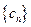
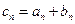 .
.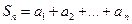 ,
,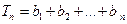 ,试比较
,试比较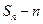 与
与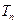 的大小,并证明;
的大小,并证明;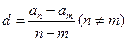 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列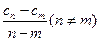 不是一个常数,但
不是一个常数,但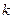 呢,若会,请求出
呢,若会,请求出 中,
中, ,则
,则



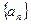 中,
中,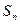 =40,
=40,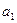 =13,d="-2" 时,n=__________.
=13,d="-2" 时,n=__________. 。
。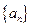 的前
的前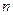 项和为
项和为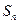 ,若
,若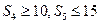 ,则
,则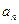 的最大值为___________.
的最大值为___________.