题目内容
12．已知集合M={x|x2-2x-3≤0}，N={x|-2＜x＜2}，则M∩N=（ ）| A． | ∅ | B． | {x|-1≤x＜2} | C． | {x|-2≤x＜-1} | D． | {x|2≤x＜3} |
分析 求出M中不等式的解集确定出M，找出M与N的交集即可．
解答 解：由M中不等式变形得：（x-3）（x+1）≤0，
解得：-1≤x≤3，即M={x|-1≤x≤3}，
∵N={x|-2＜x＜2}，
∴M∩N={x|-1≤x＜2}，
故选：B．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．4名优秀学生全部保送到3所学校去，每所学校至少去一名学生，则不同的保送方案有（ ）
| A． | 12种 | B． | 72种 | C． | 18种 | D． | 36种 |
4．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（x，1）若（$\overrightarrow{a}$+2$\overrightarrow{b}$）∥（2$\overrightarrow{a}$-2$\overrightarrow{b}$），则x的值为（ ）
| A． | 1 | B． | 2 | C． | $\frac{1}{2}$ | D． | $\frac{1}{3}$ |
1．
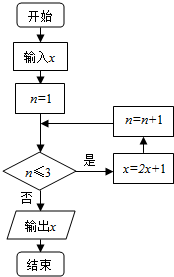已知实数x∈[1，9]，执行如图所示的程序框图，则输出的x不小于55的概率为（ ）
已知实数x∈[1，9]，执行如图所示的程序框图，则输出的x不小于55的概率为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{3}{8}$ | D． | $\frac{5}{8}$ |