题目内容
已知函数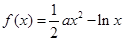 ,
,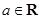 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数 在区间
在区间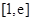 的最小值为
的最小值为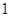 ,求
,求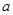 的值.
的值.
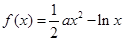 ,
,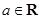 .
.(1)求函数
 的单调区间;
的单调区间;(2)若函数
 在区间
在区间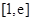 的最小值为
的最小值为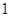 ,求
,求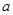 的值.
的值.(1)当 时,函数
时,函数 的单调减区间是
的单调减区间是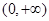 ,当
,当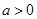 时,函数
时,函数 的单调减区间是
的单调减区间是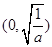 ,单调增区间为
,单调增区间为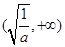 ;(2)
;(2)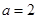 .
.
 时,函数
时,函数 的单调减区间是
的单调减区间是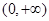 ,当
,当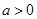 时,函数
时,函数 的单调减区间是
的单调减区间是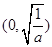 ,单调增区间为
,单调增区间为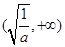 ;(2)
;(2)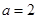 .
.试题分析:(1)求函数
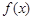 的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数
的单调区间,可利用定义,也可利用求导法,本题含有对数函数,可通过求导法来求函数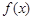 的单调区间,求函数
的单调区间,求函数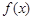 导函数
导函数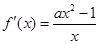 ,令
,令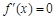 ,找出分界点,从而确定函数的单调区间,但由于含有参数
,找出分界点,从而确定函数的单调区间,但由于含有参数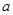 ,需对参数
,需对参数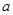 分
分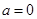 ,
,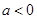 ,
,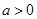 讨论,从而得函数
讨论,从而得函数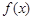 的单调区间;(2)若函数
的单调区间;(2)若函数 在区间
在区间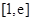 的最小值为
的最小值为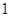 ,求
,求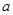 的值,求出函数
的值,求出函数 在区间
在区间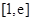 的最小值,令它等于为
的最小值,令它等于为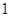 即可,由(1)可知,当
即可,由(1)可知,当 时,函数
时,函数 的单调减区间是
的单调减区间是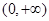 ,
, 的最小值为
的最小值为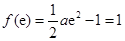 ,解出
,解出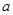 ,验证是否符合,当
,验证是否符合,当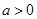 时,函数
时,函数 的单调减区间是
的单调减区间是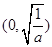 ,单调增区间为
,单调增区间为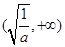 ,由于不知函数
,由于不知函数 在区间
在区间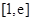 的单调性,需讨论
的单调性,需讨论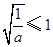 ,
,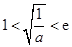 ,
,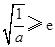 ,分别求出函数
,分别求出函数 在区间
在区间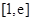 的最小值,令它等于为
的最小值,令它等于为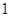 ,解出
,解出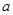 ,验证是否符合,从而得
,验证是否符合,从而得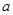 的值.
的值.试题解析:函数
 的定义域是
的定义域是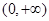 ,
, 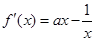
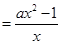 .
.(1)(1)当
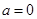 时,
时,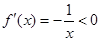 ,故函数
,故函数 在
在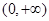 上单调递减.
上单调递减.(2)当
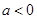 时,
时,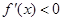 恒成立,所以函数
恒成立,所以函数 在
在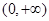 上单调递减.
上单调递减.(3)当
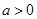 时,令
时,令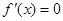 ,又因为
,又因为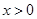 ,解得
,解得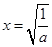 .
.①当
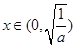 时,
时,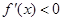 ,所以函数
,所以函数 在
在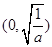 单调递减.
单调递减.②当
 时,
时,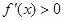 ,所以函数
,所以函数 在
在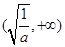 单调递增.
单调递增.综上所述,当
 时,函数
时,函数 的单调减区间是
的单调减区间是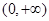 ,
,当
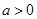 时,函数
时,函数 的单调减区间是
的单调减区间是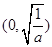 ,单调增区间为
,单调增区间为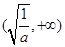 . 7分
. 7分(2)(1)当
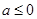 时,由(1)可知,
时,由(1)可知, 在
在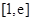 上单调递减,
上单调递减,所以
 的最小值为
的最小值为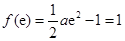 ,解得
,解得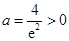 ,舍去.
,舍去.(2)当
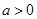 时,由(1)可知,
时,由(1)可知,①当
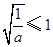 ,即
,即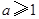 时,函数
时,函数 在
在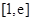 上单调递增,
上单调递增,所以函数
 的最小值为
的最小值为 ,解得
,解得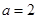 .
.②当
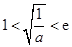 ,即
,即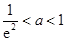 时,函数
时,函数 在
在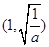 上单调递减,
上单调递减,在
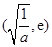 上单调递增,所以函数
上单调递增,所以函数 的最小值为
的最小值为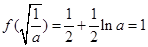 ,解得
,解得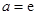 ,舍去.
,舍去.③当
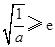 ,即
,即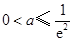 时,函数
时,函数 在
在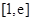 上单调递减,
上单调递减,所以函数
 的最小值为
的最小值为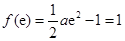 ,得
,得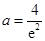 ,舍去.
,舍去.综上所述,
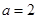 . 13分
. 13分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. 的单调区间;
的单调区间; 时,求证:
时,求证: 恒成立..
恒成立.. 在
在 处有极大值
处有极大值 .
. 的解析式;
的解析式; .
. 取到极值,求
取到极值,求 的值;
的值; 在区间
在区间 上有单调递增的区间.
上有单调递增的区间. 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,且
,且 ,
,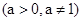 ,
, ,对于数列
,对于数列 ,任取正整数
,任取正整数 ,则前k项和大于
,则前k项和大于 的概率是( )
的概率是( )



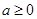 ,函数
,函数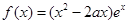 ,若
,若 在
在 上是单调减函数,则
上是单调减函数,则 的取值范围是( )
的取值范围是( )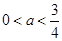
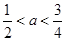
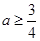
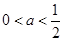
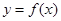 是奇函数,当
是奇函数,当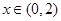 时,
时,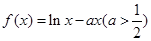 ,当
,当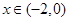 时,
时,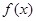 的最小值为1,则
的最小值为1,则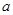 的值等于( )
的值等于( )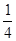
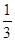
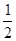
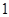
 的导函数如图所示,若
的导函数如图所示,若 为锐角三角形,则下列不等式一定成立的是( )
为锐角三角形,则下列不等式一定成立的是( )




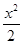 -2x+5,若对任意的x∈[-1,2],都有f(x)>m,则实数m的取值范围为________.
-2x+5,若对任意的x∈[-1,2],都有f(x)>m,则实数m的取值范围为________.