题目内容
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)当 时,求证:
时,求证: 恒成立..
恒成立..
 .
.(1)求
 的单调区间;
的单调区间;(2)当
 时,求证:
时,求证: 恒成立..
恒成立..(1)单调减区间为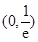 ,单调增区间为
,单调增区间为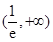 ,(2)详见解析.
,(2)详见解析.
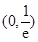 ,单调增区间为
,单调增区间为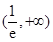 ,(2)详见解析.
,(2)详见解析.试题分析:(1)求函数单调区间,有四个步骤.一是求定义域
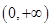 ,二是求导数为零的根,由
,二是求导数为零的根,由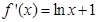 得
得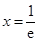 ,三是分区间讨论导数正负,当
,三是分区间讨论导数正负,当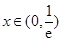 时,
时,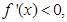 当
当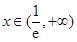 时,
时,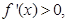 四是根据导数正负写出单调区间:单调减区间为
四是根据导数正负写出单调区间:单调减区间为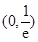 ,单调增区间为
,单调增区间为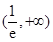 ,.(2)证明不等式恒成立问题一般化为函数最值问题.可以直接求函数
,.(2)证明不等式恒成立问题一般化为函数最值问题.可以直接求函数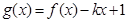 的最小值,也可
的最小值,也可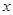 将
将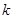 与分离,求函数
与分离,求函数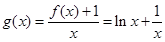 的最小值.两种思路都简洁,实质都一样,就是求最小值.
的最小值.两种思路都简洁,实质都一样,就是求最小值.试题解析:解:
(1)定义域为
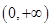 1分
1分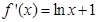 2分
2分令
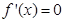 ,得
,得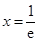 3分
3分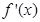 与
与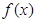 的情况如下:
的情况如下: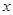 | 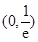 | 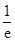 | 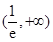 |
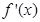 | 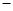 | 0 | 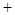 |
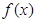 | ↘ | 极小值 | ↗ |
所以
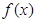 的单调减区间为
的单调减区间为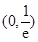 ,单调增区间为
,单调增区间为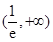 6分
6分(2)证明1:
设
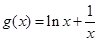 ,
,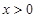 7分
7分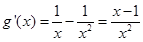 8分
8分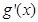 与
与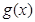 的情况如下:
的情况如下: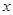 | 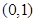 | 1 |  |
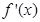 | 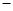 | 0 | 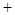 |
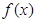 | ↘ | 极小值 | ↗ |
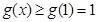 ,即
,即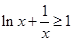 在
在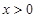 时恒成立, 10分
时恒成立, 10分所以,当
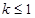 时,
时,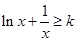 ,
,所以
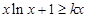 ,即
,即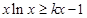 ,
,所以,当
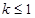 时,有
时,有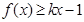 . 13分
. 13分证明2:
令
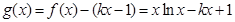 7分
7分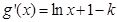 8分
8分令
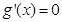 ,得
,得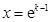 9分
9分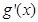 与
与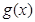 的情况如下:
的情况如下: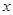 | 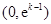 | 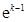 | 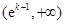 |
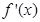 | 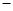 | 0 | 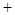 |
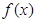 | ↘ | 极小值 | ↗ |
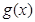 的最小值为
的最小值为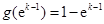 -11分
-11分当
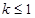 时,
时,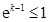 ,所以
,所以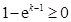
故
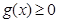 -12分
-12分即当
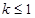 时,
时,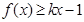 . 13分
. 13分
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
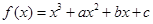 在
在 与
与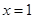 时都取得极值
时都取得极值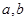 的值与函数
的值与函数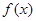 的单调区间
的单调区间 ,不等式
,不等式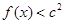 恒成立,求
恒成立,求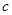 的取值范围
的取值范围 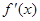 是
是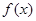 的导函数,
的导函数,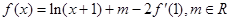 ,且函数
,且函数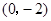 .
.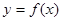 的表达式;
的表达式;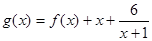 的单调区间和极值.
的单调区间和极值.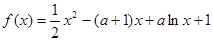
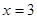 是
是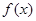 的极值点,求
的极值点,求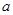 的范围,使得
的范围,使得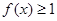 恒成立.
恒成立.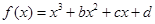 在区间
在区间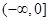 和
和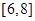 上单调递增,在
上单调递增,在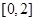 上单调递减,其图象与
上单调递减,其图象与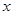 轴交于
轴交于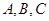 三点,其中点
三点,其中点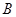 的坐标为
的坐标为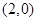 .
.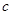 的值;
的值;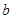 的取值范围;
的取值范围;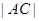 的取值范围.
的取值范围.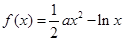 ,
,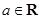 .
. 的单调区间;
的单调区间;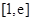 的最小值为
的最小值为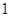 ,求
,求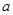 的值.
的值.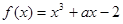 在区间
在区间 内是增函数,则实数
内是增函数,则实数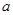 的取值范围是
的取值范围是 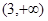
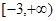
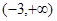
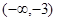
 ,求f(x)在[-1,1]上的最小值;
,求f(x)在[-1,1]上的最小值;