题目内容
已知函数 在
在 处有极大值
处有极大值 .
.
(1)求 的解析式;
的解析式;
(2)求 的单调区间;
的单调区间;
 在
在 处有极大值
处有极大值 .
.(1)求
 的解析式;
的解析式;(2)求
 的单调区间;
的单调区间;(1)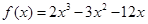
(2)单调递增区间为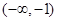 ,
,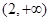 ;单调递减区间为
;单调递减区间为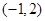
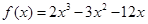
(2)单调递增区间为
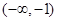 ,
,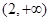 ;单调递减区间为
;单调递减区间为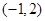
试题分析:(1)先对函数求导,根据函数在x=-1处有极大值7,得到函数在-1处的导数为0,且此处的函数值是7,列出关于字母系数的方程组,解方程组即可.
(2)根据上一问做出来的函数的解析式,是函数的导函数分别大于零和小于零,解出对应的不等式的解集,就是我们要求的函数的单调区间.
试题解析:(1)
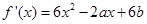 , 1分
, 1分由已知可知,
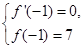 3分
3分所以
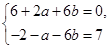 ,解得
,解得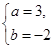 , 4分
, 4分所以
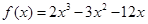 . 5分
. 5分(2)由
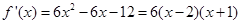 , 7分
, 7分可知:当
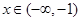 时,
时,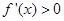 ;
;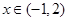 时,
时,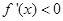 ;
;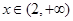 时,
时,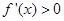 , 10分
, 10分所以
 的单调递增区间为
的单调递增区间为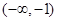 ,
,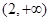 ;单调递减区间为
;单调递减区间为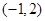 . 12分
. 12分
练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
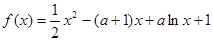
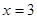 是
是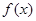 的极值点,求
的极值点,求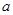 的范围,使得
的范围,使得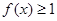 恒成立.
恒成立.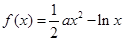 ,
,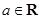 .
. 的单调区间;
的单调区间;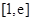 的最小值为
的最小值为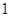 ,求
,求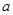 的值.
的值.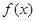 是定义在R上的奇函数,且
是定义在R上的奇函数,且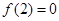 ,当x>0时,有
,当x>0时,有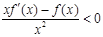 恒成立,则不等式
恒成立,则不等式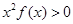 的解集是 ( )
的解集是 ( )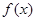 是定义在
是定义在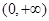 上的非负可导函数,且满足
上的非负可导函数,且满足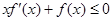 ,对任意正数
,对任意正数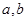 ,若
,若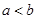 ,则必有( )
,则必有( )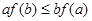
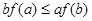
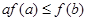
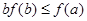
 在定义域内可导,
在定义域内可导,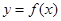 的图像如右图,则导函数
的图像如右图,则导函数 的图像可能是( )
的图像可能是( )
 对任意的
对任意的 恒成立,则
恒成立,则 .
. 的定义域为开区间
的定义域为开区间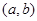 ,导函数
,导函数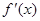 在
在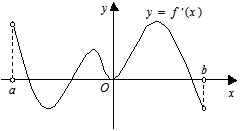
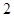 个
个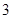 个
个 个
个