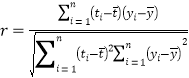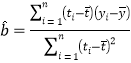题目内容
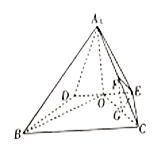
【题目】将边长分别为![]() 的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第
的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第![]() 个阴影部分图形.设前
个阴影部分图形.设前![]() 个阴影部分图形的面积的平均值为
个阴影部分图形的面积的平均值为![]() .记数列
.记数列![]() 满足:
满足: .
.

(1)求![]() 的表达式及数列
的表达式及数列![]() 的通项公式;
的通项公式;
(2)记![]()
![]() 若
若![]() ,其中
,其中![]() 为常数,且
为常数,且![]()
 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ,
,
(2) ![]()
【解析】
(1)由第一个阴影部分图形的面积为![]() ,第二个阴影部分图形的面积为
,第二个阴影部分图形的面积为![]() …第
…第![]() 个阴影部分图形的面积为
个阴影部分图形的面积为![]() ,然后求出
,然后求出![]() 即可,再利用
即可,再利用 ,求通项公式即可;
,求通项公式即可;
(2)先运算行列式可得:![]() 恒成立,再讨论当
恒成立,再讨论当![]() 时,当
时,当![]() 为偶数时, 当
为偶数时, 当![]() 为大于1的奇数时,求出
为大于1的奇数时,求出![]() 的范围即可得解.
的范围即可得解.
解:(1)由题意可得:第一个阴影部分图形的面积为![]() ,第二个阴影部分图形的面积为
,第二个阴影部分图形的面积为![]() …第
…第![]() 个阴影部分图形的面积为
个阴影部分图形的面积为![]() ,则
,则![]()
,
又 且
且![]() ,则
,则![]() ,
,![]() ,
,
当![]() 为偶数时,
为偶数时,![]() ,
,
当![]() 为大于1的奇数时,
为大于1的奇数时,![]() ,
,
即 ;
;
(2)由(1)得: ,
,
又![]()
 恒成立,即
恒成立,即![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 为偶数时,
为偶数时,![]() 恒成立,
恒成立,
即![]() ,
,
即![]() 恒成立,
恒成立,
即![]() ,
,
当![]() 为大于1的奇数时,
为大于1的奇数时,![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
即![]() 恒成立,即
恒成立,即![]() ,
,
综上所述:![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况,在本市的所有中学生中随机抽取了120名学生进行调查,现将日均自学时间小于1小时的学生称为“自学不足”者![]() 根据调查结果统计后,得到如下
根据调查结果统计后,得到如下![]() 列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为
列联表,已知在调查对象中随机抽取1人,为“自学不足”的概率为![]() .
.
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
![]() 请完成上面的列联表;
请完成上面的列联表;
![]() 根据列联表的数据,能否有
根据列联表的数据,能否有![]() 的把握认为“自学不足”与“配有智能手机”有关?
的把握认为“自学不足”与“配有智能手机”有关?
附表及公式: ![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|