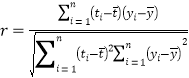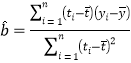题目内容
【题目】下列四个命题：①直线
的斜率
，则直线的倾斜角
；②直线：
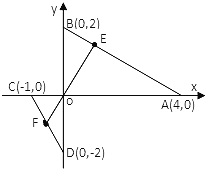
与以
、
两点为端点的线段相交，则
或
；③如果实数
满足方程
，那么
的最大值为
；④直线与椭圆
恒有公共点，则
的取值范围是
.其中正确命题的序号是______
【答案】②③
【解析】
由直线倾斜角的范围判断①错误；求出直线
恒过的定点M，再求出MA和MB所在直线的斜率判断②正确；由
的几何意义可知是连接圆上的动点和原点的连线的斜率，求出过原点的圆的切线的斜率判断③正确；由直线
恒过的定点在椭圆内部求解m的取值范围，结合圆的条件判断④错误.
对于①，由直线的倾斜角范围是
知直线的斜率
，则直线的倾斜角
错误；对于②，因为直线恒过点
，
，所以
，命题正确；对于③，方程
表示以
为圆心，以
为半径的圆，的几何意义是连接圆上的动点和原点的连线的斜率，设过原点的圆的切线方程为
，由
得
，所以的最大值为，命题正确；对于④，因为直线恒过的定点
，所以要使直线与椭圆恒有公共点则需
，解得
，但当
时，方程
不是椭圆，所以命题错误.
故答案为：②③
练习册系列答案
相关题目
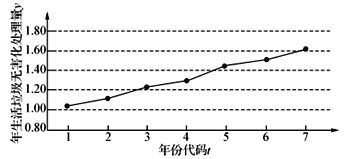
【题目】一般来说，一个人脚掌越长，他的身高就越高，现对10名成年人的脚掌
与身高
进行测量，得到数据（单位：cm）作为样本如表所示：
脚掌长（ | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
身高（ | 141 | 146 | 154 | 160 | 169 | 176 | 181 | 188 | 197 | 203 |
（1）在上表数据中，以“脚掌长”为横坐标，“身高”为纵坐标，作出散点图后，发现散点在一条直线附近，试求“身高”与“脚掌长”之间的线性回归方程
；
（2）若某人的脚掌长为26.5cm，试估计此人的身高；
（3）在样本中，从身高180cm以上的4人中随机抽取2人进行进一步的分析，求所抽取的2人中至少有1人身高在190cm以上的概率.
（参考数据：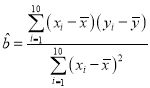
，
，
，
，
）
