题目内容
【题目】已知椭圆
的离心率为
，其中一个焦点F在直线
上.
（1）求椭圆C的方程；
（2）若直线
和直线
与椭圆分别相交于点
、
、
、
，求
的值;
（3）若直线
与椭圆交于P，Q两点，试求
面积的最大值.
【答案】（1）
；
（2）8；
（3）1；
【解析】
（1）根据题意得到椭圆的一个焦点即为直线与
轴的交点，从而求得
，结合离心率，求得
的值，进而求得
，得到椭圆的方程；
（2）根据椭圆的定义和椭圆的对称性，得到结果；
（3）将直线方程和椭圆的方程联立，利用弦长公式和点到直线的距离，利用面积公式写出三角形的面积，利用基本不等式求得最值，注意满足判别式大于零的条件.
（1）椭圆的一个焦点即为直线与轴的交点
，所以，
又离心率为
则
,
，所以椭圆方程为；
（2）设椭圆的另一个焦点为
, 由已知得:
（3）联立直线
与椭圆方程得,
，
令
，得
设方程
的两根为
，
则
，
，
由弦长公式得，
，点
到直线
的距离
，
当且仅当
， 即
或
时取等号，而或满足，
所以三角形
面积的最大值为1.
【题目】汕尾市基础教育处为调查在校中学生每天放学后的自学时间情况，在本市的所有中学生中随机抽取了120名学生进行调查，现将日均自学时间小于1小时的学生称为“自学不足”者
根据调查结果统计后，得到如下
列联表，已知在调查对象中随机抽取1人，为“自学不足”的概率为
．
非自学不足 | 自学不足 | 合计 | |
配有智能手机 | 30 | ||
没有智能手机 | 10 | ||
合计 |
请完成上面的列联表；
根据列联表的数据，能否有
的把握认为“自学不足”与“配有智能手机”有关？
附表及公式: 
，其中
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】为了了解
地区足球特色学校的发展状况，某调查机构得到如下统计数据：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
（Ⅰ）根据上表数据，计算
与
的相关系数
，并说明与的线性相关性强弱（已知：
，则认为与线性相关性很强；
，则认为与线性相关性一般；
，则认为与线性相关性较弱）；
（Ⅱ）求关于的线性回归方程，并预测地区2019年足球特色学校的个数（精确到个）
参考公式：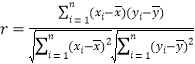
，
，
，
，
，
.
