题目内容
2.某几何体的三视图如图所示,按图中所给的尺寸,该几何体的体积为( )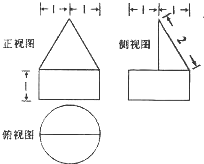
| A. | $\frac{\sqrt{3}π}{6}$+1 | B. | $\frac{\sqrt{3}π}{6}$+π | C. | $\frac{\sqrt{3}π}{3}$+π | D. | $\frac{\sqrt{3}π}{3}$+1 |
分析 由已知的三视图可得:该几何体是一个圆柱与半圆锥的组合体,分别计算体积,相加可得答案.
解答 解:由已知的三视图可得:该几何体是一个圆柱与半圆锥的组合体,
圆柱的底面半径为1,高为1,故圆柱的体积为:π,
半圆锥的底面半径为1,高为$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
故半圆锥的体积为:$\frac{\sqrt{3}π}{6}$,
故组合体的体积为:$\frac{\sqrt{3}π}{6}+π$,
故选:B.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
12.若函数f(x)满足f(2)=1且f(x+3)=2f(x),则f(2015)=( )
| A. | 2670 | B. | 2671 | C. | 2672 | D. | 2673 |
10.吉安市某工厂车间加工零件的个数x与所花费的时间y之间的线性回归方程为y=0.01x-0.5,则加工600个零件大约需要时间为( )h.
| A. | 0.5 | B. | 3.5 | C. | 5.5 | D. | 6.5 |
7.已知F1、F2为椭圆的两个焦点,以线段F1F2为一边的正方形ABF2F1与椭圆交于M,N两点,且M,N分别为边AF1,BF2的中点,则椭圆的离心率为( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{5}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
11.下列向量中,可以作为基底的是( )
| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(1,-2) | B. | $\overrightarrow{{e}_{1}}$=(2,-3),$\overrightarrow{{e}_{2}}$=(-$\frac{1}{2}$,$\frac{3}{4}$) | ||
| C. | $\overrightarrow{{e}_{1}}$=(3,5),$\overrightarrow{{e}_{2}}$=(6,10) | D. | $\overrightarrow{{e}_{1}}$=(1,-2),$\overrightarrow{{e}_{2}}$=(5,7) |
12.已知0<a<1,则方程ax-|logax|=0的实根个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |