题目内容

20．如图，正方体ABC-A1B1C1D1中，点F为A1D的中点．
（Ⅰ）求证：A1B∥平面AFC；
（Ⅱ）求证：平面A1B1D⊥平面AFC．

分析 （1）根据线面平行的判定定理只需证明直线A1B平行平面AFC内的直线FO即可；
（2）根据面面垂直判定定理只需证明AF⊥平面A1B1CD即可．

解答 证明：（1）连接BD交AC于点O，连接FO，
则点O是BD的中点．
∵点F为A1D的中点，∴A1B∥FO．
又A1B?平面AFC，FO?平面AFC，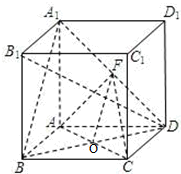
∴A1B∥平面AFC．
（2）在正方体ABCD-A1B1C1D1中，
连接B1D．∵AC⊥BD，AC⊥BB1，
∴AC⊥平面B1BD，AC⊥B1D．
又∵CD⊥平面A1ADD1，AF?平面A1ADD1，
∴CD⊥AF．
又∵AF⊥A1D，
∴AF⊥平面A1B1CD．
∵AF?平面AFC．
∴平面A1B1CD⊥平面AFC，
即平面A1B1D⊥平面AFC．

点评 本题考查平面与平面垂直的判定，直线与平面平行的判定，考查空间想象能力，要求熟练掌握相应的判定定理和性质定理．

练习册系列答案
相关题目
2．已知数列{an}的前n项和为Sn，a1=$\frac{1}{4}$，Sn=Sn-1+an-1+$\frac{1}{2}$（n∈N*，n≥2），数列{bn}满足b1=2，bn+1=3bn+2，
（1）分别求数列{an}和{bn}通项公式；
（2）若数列{cn}=an-$\frac{10}{{b}_{n}+1}$，数列{cn}的前n项和为Tn，求数列{Tn}的最小值．
11．设函数fk（x）=xk+bx+c（k∈N*，b，c∈R），g（x）=logax（a＞0，且a≠1）
（1）若b+c=1，且fk（1）=g（$\frac{1}{4}$），求a的值；
（2）记函数f2（x）在[-1，1]上的最大值为M，最小值为m，求M-m≤4时b的取值范围；
（3）判断是否存在大于1的实数a，使得对任意x1∈[a，2a]，都有x2∈[a，a2]满足等式g（x1）+g（x2）=p，且满足该等式的常数p的取值唯一？若存在，求出所有符合条件的a的值；若不存在，请说明理由．
8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，过其左焦点且与其长轴垂直的椭圆C的弦长为1．
（1）求椭圆C的方程
（2）求与椭圆C交于两点且过点（0，$\sqrt{3}$）的直线l的斜率k的取值范围．
15．在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立坐标系．已知点A的极坐标为（$\sqrt{2}$，$\frac{π}{4}$），直线L的直角坐标方程为x+y=a，且点A在直线上L．
（1）求a的值；
（2）圆C的参数方程为$\left\{{\begin{array}{l}{x=1+cosα}\\{y=sinα}\end{array}}$，（α为参数），试判断直线L与圆C的位置关系并说明理由．
5．已知函数f（x）=$\left\{\begin{array}{l}{0，x=0}\\{\frac{lnx}{x}，x＞0}\end{array}\right.$，g（x）=|sin$\frac{π}{2}$x|，则f（x）与g（x）的图象在区间[0，6]上的交点个数为（　　）
A．5B．6C．7D．8
12．若函数f（x）满足f（2）=1且f（x+3）=2f（x），则f（2015）=（　　）
A．2670B．2671C．2672D．2673
9．椭圆ax2+by2=1与直线y=1-x交于A、B两点，过原点与线段AB中点的直线的斜率为$\frac{\sqrt{3}}{2}$，则$\frac{b}{a}$值为（　　）
A．$\frac{\sqrt{3}}{2}$B．$\frac{2\sqrt{3}}{3}$C．$\frac{9\sqrt{3}}{2}$D．$\frac{2\sqrt{3}}{27}$
10．吉安市某工厂车间加工零件的个数x与所花费的时间y之间的线性回归方程为y=0.01x-0.5，则加工600个零件大约需要时间为（　　）h．
A．0.5B．3.5C．5.5D．6.5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网