Question

6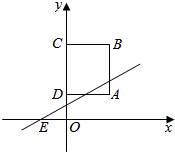．如图：点A的坐标为（2，1），正方形ABCD的点C、点D都在y轴上．从背面完全一样，正面分别写有数字-2，-1，0，1，2的五张牌中任取一张，将其正面的数字作为k值，则能使一次函数y=kx+b的图象过经点E（-1，0），且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$．

Answer 1

分析 根据条件先求出A，B，C，D的坐标，根据斜率公式求出直线的斜率，然后利用古典概型的概率公式进行求解即可．

解答 解：∵点A的坐标为（2，1），
∴正方形ABCD的边长为2，
则D（0，1），C（0，3），B（2，3），
∵能使一次函数y=kx+b的图象过经点E（-1，0），且与正方形ABCD恰有两个公共点，
∴满足k_AE＜k＜k_EC，
∵k_AE=$\frac{0-1}{-1-2}$=$\frac{1}{3}$，k_EC=$\frac{3-0}{0-（-1）}=3$，
∴$\frac{1}{3}$＜k＜3，
则满足条件的k=1，2，
故对应的概率P=$\frac{2}{5}$，
故答案为：$\frac{2}{5}$

点评 本题主要考查概率的计算，直线斜率的求解，根据条件求出A，B，C，D的坐标以及求出满足条件的k的取值范围是解决本题的关键．