对于任意实数x.代数式$\frac{1}{2}{x^2}$-3x+5的值是一个( )A．非负数B．正数C．负数D．整数题目和参考答案——青夏教育精英家教网—

题目内容

1．对于任意实数x，代数式$\frac{1}{2}{x^2}$-3x+5的值是一个（　　）

A．

非负数

B．

正数

C．

负数

D．

整数

分析对代数式配方，根据二次函数的性质求出代数式的范围，即可得到答案．

解答解：因为$\frac{1}{2}{x^2}$-3x+5=$\frac{1}{2}{（x}^{2}-6x）+5$=$\frac{1}{2}{（x-3）}^{2}+\frac{1}{2}$$≥\frac{1}{2}$恒成立，
所以对于任意实数x，代数式$\frac{1}{2}{x^2}$-3x+5的值是一个正数，
故选：B．

点评本题考查二次函数的性质，以及配方法的应用，属于基础题．

练习册系列答案

12．若a、b是正常数，a≠b，x、y∈（0，+∞），则$\frac{{a}^{2}}{x}$+$\frac{{b}^{2}}{y}$≥$\frac{{（a+b）}^{2}}{x+y}$，当且仅当$\frac{a}{x}$=$\frac{b}{y}$时上式取等号．利用以上结论，可以得到函数f（x）=$\frac{4}{x}$+$\frac{9}{1-2x}$（x∈（0，$\frac{1}{2}$））的最小值为17+12$\sqrt{2}$．

9．不等式x²-12＜x的解是（-3，4）．

16．

如图，已知圆（x-2）²+y²=$\frac{4}{9}$是椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的内接△ABC的内切圆，其中A为椭圆C的左顶点，且椭圆C的离心率为$\frac{{\sqrt{15}}}{4}$，则此椭圆的标准方程为$\frac{x^2}{16}+{y^2}=1$．

6．

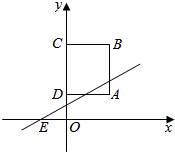如图：点A的坐标为（2，1），正方形ABCD的点C、点D都在y轴上．从背面完全一样，正面分别写有数字-2，-1，0，1，2的五张牌中任取一张，将其正面的数字作为k值，则能使一次函数y=kx+b的图象过经点E（-1，0），且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$．

13．函数y=Asin（ωx+φ）（0＜φ＜π）在一个周期内的图象如图，此函数的解析式为y=2sin（2x+$\frac{2π}{3}$）

13．计算：sin$\frac{7π}{3}$-$\frac{\sqrt{2}}{2}$cos$\frac{11π}{4}$+$\frac{4}{3}$sin²$\frac{π}{6}$-cos$\frac{4}{3}$π．

14．用反证法证明命题“三角形的内角至多有一个钝角”时，假设正确的是（　　）

	A．	假设至少有一个钝角
	B．	假设至少有两个钝角
	C．	假设没有一个钝角
	D．	假设没有一个钝角或至少有两个钝角

试题分类