题目内容
11.(理科)设f(x)是定义在R上的不恒为零的偶函数,且当x>0时,f(x)是单调函数,则满足f(x)=f($\frac{x+3}{x+4}$)的所有x之和为( )| A. | -8 | B. | -3 | C. | 3 | D. | 8 |
分析 f(x)为偶函数推出f(-x)=f(x),x>0时f(x)是单调函数推出f(x)不是周期函数.所以若f(a)=f(b)⇒a=b或a=-b,再利用根与系数的关系进行求解;
解答 解:∵f(x)为偶函数,且当x>0时f(x)是单调函数,
又满足f(x)=f($\frac{x+3}{x+4}$),
∴x=$\frac{x+3}{x+4}$或-x=$\frac{x+3}{x+4}$,
可得,x2+3x-3=0或x2+5x+3=0,
∴x1+x2=-3或x3+x4=-5,
∴x1+x2+x3+x4=-3-5=-8,
故选:A
点评 本题属于函数性质的综合应用,解决此类题型要注意变换自变量与函数值的关系,利用函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
2.不等式x>x2的解集是( )
| A. | {x|x<0} | B. | {x|x>0} | C. | {x|x<1} | D. | {x|0<x<1} |
16.在周长为16的△PMN中,MN=6,则$\overrightarrow{PM}$•$\overrightarrow{PN}$的取值范围是( )
| A. | [7,16) | B. | (7,16] | C. | [7,16] | D. | (7,16) |
3.若|x|≤1时都有|ax+b|≤1,则不等必成立的是( )
| A. | |a|≤|b|≤1 | B. | |b|≤|a|≤1 | C. | |a|≤1,|b|≤1 | D. | |a|+|b|≤1 |
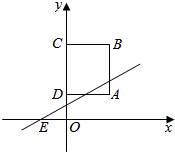 如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.
如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.