题目内容
14.在△ABC中,内角A,B,C的对边分别为a,b,c.已知$\frac{cosA-2cosC}{cosB}=\frac{2c-a}{b}$.(1)求$\frac{sinC}{sinA}$的值;
(2)若cosB=$\frac{1}{4}$,△ABC的周长为5,求b的长及△ABC的面积;
(3)若a=1,求A的最大值及此时△ABC的形状.
分析 (1)由正弦定理,三角形内角和定理化简已知等式可得sinC=2sinA,即可得解.
(2)由(1)及正弦定理有$\frac{c}{a}=2$,结合周长为5,可得b=5-3a,由余弦定理即可解得a,b.c,又$cosB=\frac{1}{4}$,可求sinB,由三角形面积公式即可得解.
(3)由余弦定理与基本不等式可得$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{{{b^2}+3}}{4b}=\frac{1}{4}(b+\frac{3}{b})≥\frac{1}{4}×2\sqrt{3}=\frac{{\sqrt{3}}}{2}$,结合角的范围0<A<π,可得$0<A≤\frac{π}{6}$,当且仅当$b=\frac{3}{b}$即$b=\sqrt{3}$时${A_{max}}=\frac{π}{6}$.
解答 解:(1)由正弦定理得a=2RsinA,b=2RsinB,c=2RsinC,
所以$\frac{cosA-2cosC}{cosB}=\frac{2c-a}{b}$=$\frac{2sinC-sinA}{sinB}$,
即sinBcosA-2sinBcosC=2sinCcosB-sinAcosB,
即有sin(A+B)=2sin(B+C),
即sinC=2sinA,
所以$\frac{sinC}{sinA}$=2.
(2)由(1)知$\frac{sinC}{sinA}$=2,所以有$\frac{c}{a}=2$,即c=2a,又因为△ABC的周长为5,
所以b=5-3a,由余弦定理得:b2=c2+a2-2accosB,即${(5-3a)^2}={(2a)^2}+{a^2}-4{a^2}×\frac{1}{4}$,解得a=1,
所以b=2.c=2,又因为$cosB=\frac{1}{4}$,所以$sinB=\frac{{\sqrt{15}}}{4}$,
故△ABC的面积为$\frac{1}{2}acsinB=\frac{1}{2}×1×2×\frac{\sqrt{15}}{4}$=$\frac{\sqrt{15}}{4}$.
(3)∵$\frac{sinC}{sinA}=2$,a=1,
∴c=2
∴$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{{{b^2}+3}}{4b}=\frac{1}{4}(b+\frac{3}{b})≥\frac{1}{4}×2\sqrt{3}=\frac{{\sqrt{3}}}{2}$,
∵0<A<π,
∴$0<A≤\frac{π}{6}$,当且仅当$b=\frac{3}{b}$即$b=\sqrt{3}$时${A_{max}}=\frac{π}{6}$,
此时a2+b2=c2,△ABC为直角三角形.
点评 本题主要考查了正弦定理,余弦定理,三角形面积公式,基本不等式的应用,属于基本知识的考查.

| A. | 4 | B. | 3 | C. | 2 | D. | 1 |

| A. | 3 | B. | 8 | C. | 12 | D. | 20 |
| A. | {x|x<0} | B. | {x|x>0} | C. | {x|x<1} | D. | {x|0<x<1} |
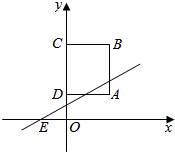 如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.
如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.