题目内容
16.已知数列{an}满足$\frac{{a}_{n}}{n}$-$\frac{{a}_{n-1}}{n-1}$=$\frac{1}{n(n-1)}$ (n≥2),a1=1.(1)设bn=$\frac{{a}_{n}}{n}$,求数列{bn}的通项公式;
(2)求数列{an}的前n项和Sn.
分析 (Ⅰ)通过裂项可知$\frac{{a}_{n}}{n}$-$\frac{{a}_{n-1}}{n-1}$=$\frac{1}{n-1}$-$\frac{1}{n}$,进而利用累加法计算即得结论;
(Ⅱ)通过(Ⅰ)知an=2n-1,利用等差数列的求和公式计算即得结论.
解答 解:(Ⅰ)由已知得:$\frac{{a}_{n}}{n}$-$\frac{{a}_{n-1}}{n-1}$=$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,
∴$\frac{{a}_{n-1}}{n-1}$-$\frac{{a}_{n-2}}{n-2}$=$\frac{1}{n-2}$-$\frac{1}{n-1}$,
…
$\frac{{a}_{2}}{2}$-$\frac{{a}_{1}}{1}$=1-$\frac{1}{2}$,
以上各式相加得$\frac{{a}_{n}}{n}$-$\frac{{a}_{1}}{1}$=1-$\frac{1}{n}$,
即bn=$\frac{{a}_{n}}{n}$=$\frac{{a}_{1}}{1}$+1-$\frac{1}{n}$=2-$\frac{1}{n}$;
(Ⅱ)由(Ⅰ)知$\frac{{a}_{n}}{n}$=2-$\frac{1}{n}$,即an=2n-1,
∴数列{an}是首项为1、公差为2的等差数列,
∴Sn=$\frac{n(1+2n-1)}{2}$=n2.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
7.设α、β、γ满足0<α<β<γ<2π,若对任意x∈R,cos(x+α)+cos(x+β)+cos(x+γ)=0恒成立,则γ-α的值是( )
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$或$\frac{4π}{3}$ | D. | 无法确定 |
4.设F为抛物线y2=4x的焦点,直线l与其交于A,B两点,与x轴交于P点,且以AB为直径的圆过原点O,则$\overrightarrow{OF}•\overrightarrow{FP}$等于( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
5.阅读如图所示的程序框图,当输入的值为3时,输出的结果是( )
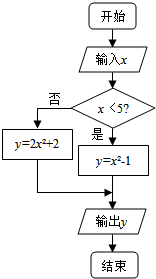

| A. | 3 | B. | 8 | C. | 12 | D. | 20 |
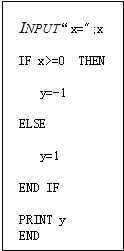
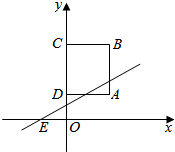 如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.
如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.