题目内容
18. 如图,在平面直角坐标系xoy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xoy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.(1)若点A的纵坐标是$\frac{4}{5}$,点B的纵坐标是$\frac{12}{13}$,求sin(α+β)的值;
(2)若$|\overrightarrow{AB}|=\frac{3}{2}$,求$|\overrightarrow{OA}+2\overrightarrow{OB}|$的值.
分析 (1)由任意角的三角函数的定义和两角和的正弦公式,计算即可得到所求;
(2)运用向量的数量积的性质:向量的平方即为模的平方,计算即可得到.
解答 解:(1)由三角函数的定义得,$sinα=\frac{4}{5}$,$sinβ=\frac{12}{13}$.
由角α、β的终边分别在第一和第二象限,
所以$cosα=\frac{3}{5}$,$cosβ=-\frac{5}{13}$,
所以$sin({α+β})=sinαcosβ+cosαsinβ=\frac{16}{65}$;
(2)$|\overrightarrow{AB}|=|\overrightarrow{OB}-\overrightarrow{OA}|$,
则有$|\overrightarrow{OB}-\overrightarrow{OA}{|^2}={\overrightarrow{OB}^2}-2\overrightarrow{OB}•\overrightarrow{OA}+{\overrightarrow{OA}^2}=2-2\overrightarrow{OB}•\overrightarrow{OA}$,
又$|\overrightarrow{AB}|=\frac{3}{2}$,
故$2-2\overrightarrow{OB}•\overrightarrow{OA}=\frac{9}{4}$,
得$\overrightarrow{OA}•\overrightarrow{OB}=-\frac{1}{8}$,
$|\overrightarrow{OA}+2\overrightarrow{OB}{|^2}={\overrightarrow{OA}^2}+4\overrightarrow{OA}•\overrightarrow{OB}+4{\overrightarrow{OB}^2}=5+4\overrightarrow{OB}•\overrightarrow{OA}=\frac{9}{2}$,
即$|\overrightarrow{OA}+2\overrightarrow{OB}|$=$\frac{3\sqrt{2}}{2}$.
点评 本题考查向量向量的数量积的性质和运用,同时考查任意角三角函数的定义和两角和的正弦公式的运用,属于中档题.

| A. | 3 | B. | 8 | C. | 12 | D. | 20 |
| A. | |a|≤|b|≤1 | B. | |b|≤|a|≤1 | C. | |a|≤1,|b|≤1 | D. | |a|+|b|≤1 |
| A. | 1 | B. | 3 | C. | 2 | D. | -2 |
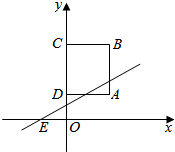 如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.
如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.