题目内容
1.定义[x]表示不超过x的最大整数(x∈R),如:[-1.3]=-2.[0.8]=0,[3.4]=3.定义{x}=x-[x].(1)$\left\{{\frac{999}{1000}}\right\}+\left\{{\frac{{{{999}^2}}}{1000}}\right\}+\left\{{\frac{{{{999}^3}}}{1000}}\right\}+$…+$\left\{{\frac{{{{999}^{1000}}}}{1000}}\right\}$=500;
(2)若x∈[0,316],函数f(x)=sin2[x]+sin2{x}-1的零点个数为m,则m=101.
分析 (1)由 $\frac{{999}^{n}}{1000}$=$\frac{{(1000-1)}^{n}}{1000}$=$\frac{{C}_{n}^{0}{•1000}^{1000}{-C}_{n}^{1}{•1000}^{999}+…{+C}_{n}^{n-1}{•1000•(-1)}^{n-1}{+(-1)}^{n}}{1000}$可得$\{\frac{{999}^{2}}{1000}\}$=$\frac{1}{1000}$,{$\frac{{999}^{3}}{1000}$}=$\frac{999}{1000}$,{$\frac{{999}^{4}}{1000}$}=1,…,从而求得;
(2)由函数f(x)=sin2[x]+sin2{x}-1=0可得2[x]-x=$\frac{π}{2}$+kπ(k∈Z),作函数y=2[x]-x的图象,利用数形结合求解即可.
解答 解:(1)$\{\frac{999}{1000}\}$=$\frac{999}{1000}$,$\frac{{999}^{2}}{1000}$=$\frac{{(1000-1)}^{2}}{1000}$=1000-2+$\frac{1}{1000}$,∴$\{\frac{{999}^{2}}{1000}\}$=$\frac{1}{1000}$.
再由 $\frac{{999}^{n}}{1000}$=$\frac{{(1000-1)}^{n}}{1000}$=$\frac{{C}_{n}^{0}{•1000}^{1000}{-C}_{n}^{1}{•1000}^{999}+…{+C}_{n}^{n-1}{•1000•(-1)}^{n-1}{+(-1)}^{n}}{1000}$,
可得 {$\frac{{999}^{3}}{1000}$}=$\frac{999}{1000}$,{$\frac{{999}^{4}}{1000}$}=1,…,
∴$\left\{{\frac{999}{1000}}\right\}+\left\{{\frac{{{{999}^2}}}{1000}}\right\}+\left\{{\frac{{{{999}^3}}}{1000}}\right\}+$…+$\left\{{\frac{{{{999}^{1000}}}}{1000}}\right\}$=($\frac{999}{1000}$+$\frac{1}{1000}$)+($\frac{999}{1000}$+1$\frac{1}{1000}$)+…($\frac{999}{1000}$+$\frac{1}{1000}$)=500,
故答案为:500.
(2)∵函数f(x)=sin2[x]+sin2{x}-1=0,
∴sin2[x]=cos2{x}=cos2(x-[x]),
∴2[x]=x+$\frac{π}{2}$+kπ(k∈Z),
∴2[x]-x=$\frac{π}{2}$+kπ(k∈Z),
作函数y=2[x]-x的图象如下,
结合图象可知,
若x∈[0,316],则2[x]-x∈[-1,315],
故$\frac{π}{2}$,$\frac{π}{2}$+π,$\frac{π}{2}$+2π,…,$\frac{π}{2}$+100π∈[-1,315],
故m=101;
故答案为:101.
点评 本题考查了二项式定理的应用及数列求和方法的应用,同时考查了方程的根与函数的关系应用,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 1 | B. | 3 | C. | 2 | D. | -2 |
| A. | m<$\frac{17}{16}$ | B. | m>$\frac{17}{16}$ | C. | m≤$\frac{17}{16}$ | D. | m>0 |
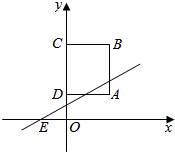 如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.
如图:点A的坐标为(2,1),正方形ABCD的点C、点D都在y轴上.从背面完全一样,正面分别写有数字-2,-1,0,1,2的五张牌中任取一张,将其正面的数字作为k值,则能使一次函数y=kx+b的图象过经点E(-1,0),且与正方形ABCD恰有两个公共点的概率是$\frac{2}{5}$.