题目内容
(本题满分18分)本题共3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知数列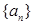 满足
满足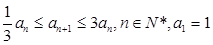 .
.
(1)若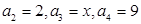 ,求
,求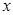 的取值范围;
的取值范围;
(2)若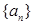 是公比为
是公比为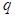 等比数列,
等比数列,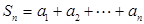 ,
,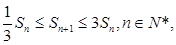 求
求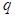 的取值范围;
的取值范围;
(3)若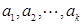 成等差数列,且
成等差数列,且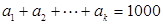 ,求正整数
,求正整数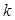 的最大值,以及
的最大值,以及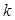 取最大值时相应数列
取最大值时相应数列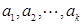 的公差.
的公差.
已知数列
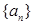 满足
满足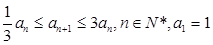 .
.(1)若
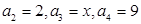 ,求
,求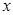 的取值范围;
的取值范围;(2)若
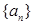 是公比为
是公比为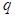 等比数列,
等比数列,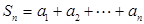 ,
,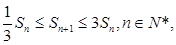 求
求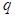 的取值范围;
的取值范围;(3)若
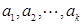 成等差数列,且
成等差数列,且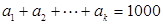 ,求正整数
,求正整数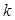 的最大值,以及
的最大值,以及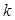 取最大值时相应数列
取最大值时相应数列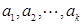 的公差.
的公差.(1)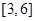 ;(2)
;(2)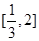 ;(3)
;(3)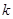 的最大值为1999,此时公差为
的最大值为1999,此时公差为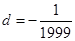 .
.
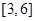 ;(2)
;(2)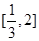 ;(3)
;(3)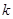 的最大值为1999,此时公差为
的最大值为1999,此时公差为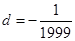 .
.试题分析:(1)比较容易,只要根据已知列出不等式组
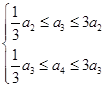 ,即可解得;(2)首先由已知得不等式
,即可解得;(2)首先由已知得不等式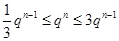 ,即
,即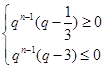 ,可解得
,可解得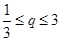 。又有条件
。又有条件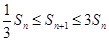 ,这时还要忘记分类讨论,
,这时还要忘记分类讨论,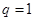 时,
时,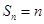 ,满足
,满足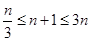 ,当
,当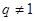 时,有
时,有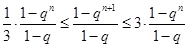 ,解这不等式时,分类,分
,解这不等式时,分类,分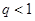 和
和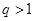 进行讨论;(3)由已知可得∴
进行讨论;(3)由已知可得∴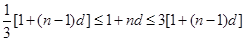 ,∴
,∴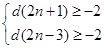 ,
,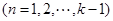 ,这样我们可以首先计算出
,这样我们可以首先计算出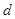 的取值范围是
的取值范围是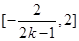 ,再由
,再由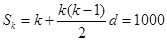 ,可得
,可得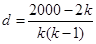 ,从而
,从而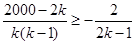 ,解得
,解得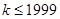 ,即
,即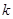 最大值为1999,此时可求得
最大值为1999,此时可求得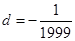 .
.试题解析:(1)由题得,
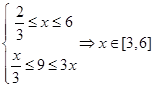
(2)由题得,∵
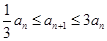 ,且数列
,且数列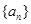 是等比数列,
是等比数列,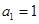 ,
,∴
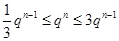 ,∴
,∴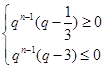 ,∴
,∴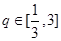 .
.又∵
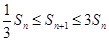 ,∴当
,∴当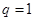 时,
时,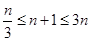 对
对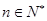 恒成立,满足题意.
恒成立,满足题意.当
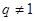 时,
时,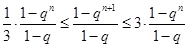
∴①当
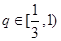 时,
时,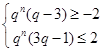 ,由单调性可得,
,由单调性可得,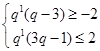 ,解得,
,解得,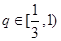
②当
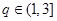 时,
时,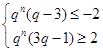 ,由单调性可得,
,由单调性可得,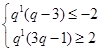 ,解得,
,解得,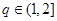
(3)由题得,∵
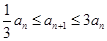 ,且数列
,且数列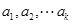 成等差数列,
成等差数列,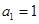 ,
,∴
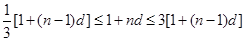 ,∴
,∴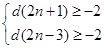 ,
,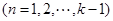 ,
,所以
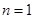 时,
时,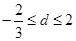 ,
,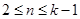 时,
时,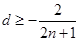 ,所以
,所以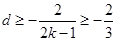 .
.∴
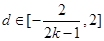
又∵
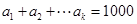 ,∴
,∴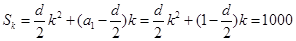
∴
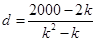 ,∴
,∴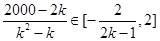 ,解得,
,解得,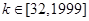 ,
,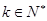
∴
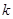 的最大值为1999,此时公差为
的最大值为1999,此时公差为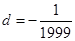 .
.【考点】解不等式(组),数列的单调性,分类讨论,等差(比)数列的前
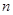 项和.
项和.
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示 项和.
项和. 及
及 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求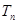 .
. 是等差数列,满足
是等差数列,满足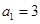 ,
,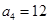 ,数列
,数列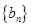 满足
满足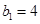 ,
,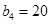 ,且
,且 是等比数列.
是等比数列.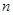 项和.
项和.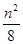 +
+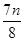
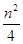 +
+
 +
+
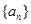 中,
中,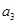 =2,
=2,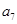 =1,若
=1,若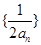 为等差数列,则公差等于( )
为等差数列,则公差等于( )



 中,a1=1,d=3,an=298,则n的值等于( ).
中,a1=1,d=3,an=298,则n的值等于( ). 中,
中, ,则数列
,则数列 等于
等于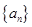 中,
中,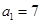 ,公差为
,公差为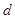 ,前
,前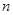 项和为
项和为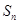 ,当且仅当
,当且仅当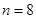 时
时