题目内容
(14分)设各项均为正数的数列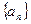 的前n项和为
的前n项和为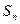 ,已知
,已知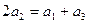 ,数
,数
列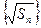 是公差为
是公差为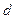 的等差数列。
的等差数列。
(1)求数列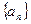 的通项公式(用
的通项公式(用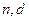 表示);
表示);
(2)设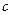 为实数,对满足
为实数,对满足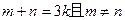 的任意正整数
的任意正整数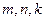 ,不等式
,不等式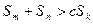 都成立。求证:
都成立。求证: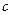 的最大值为
的最大值为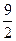 。
。
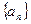 的前n项和为
的前n项和为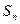 ,已知
,已知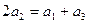 ,数
,数列
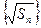 是公差为
是公差为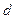 的等差数列。
的等差数列。(1)求数列
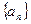 的通项公式(用
的通项公式(用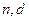 表示);
表示);
(2)设
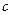 为实数,对满足
为实数,对满足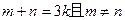 的任意正整数
的任意正整数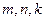 ,不等式
,不等式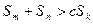 都成立。求证:
都成立。求证: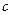 的最大值为
的最大值为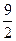 。
。解:(1)由题意知: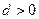 ,
,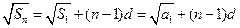
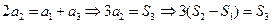 ,
,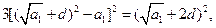
化简,得: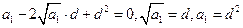
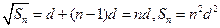 ,
,
当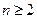 时,
时,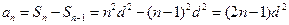 ,适合
,适合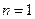 情形。
情形。
故所求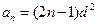
(2)(方法一)
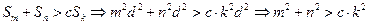 ,
,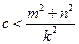 恒成立。
恒成立。
又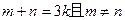 ,
, ,
,
故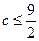 ,即
,即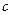 的最大值为
的最大值为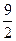 。
。
(方法 二)由
二)由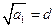 及
及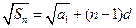 ,得
,得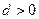 ,
,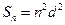 。
。
于是,对满足题设的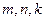 ,
,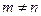 ,有
,有
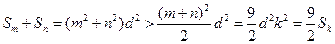 。
。
所以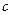 的最大值
的最大值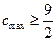 。
。
另一方面,任取实数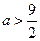 。设
。设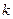
 为偶数,令
为偶数,令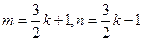 ,则
,则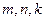 符合条件,
符合条件,
且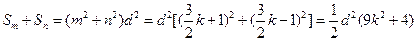 。
。
于是,只要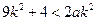 ,即当
,即当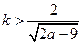 时,
时,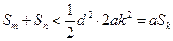 。
。
所以满足条件的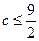 ,从而
,从而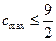 。因此
。因此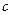 的最大值为
的最大值为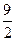 。
。
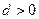 ,
,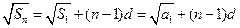
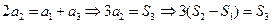 ,
,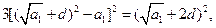
化简,得:
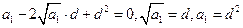
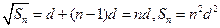 ,
,当
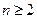 时,
时,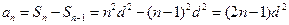 ,适合
,适合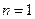 情形。
情形。故所求
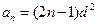
(2)(方法一)
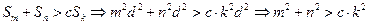 ,
,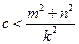 恒成立。
恒成立。又
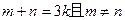 ,
, ,
,故
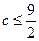 ,即
,即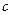 的最大值为
的最大值为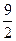 。
。(方法
 二)由
二)由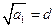 及
及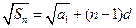 ,得
,得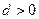 ,
,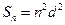 。
。于是,对满足题设的
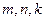 ,
,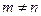 ,有
,有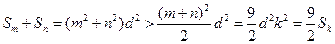 。
。所以
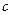 的最大值
的最大值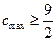 。
。另一方面,任取实数
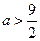 。设
。设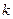
 为偶数,令
为偶数,令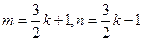 ,则
,则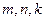 符合条件,
符合条件,且
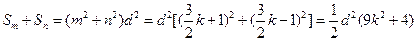 。
。于是,只要
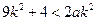 ,即当
,即当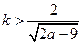 时,
时,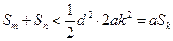 。
。所以满足条件的
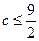 ,从而
,从而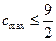 。因此
。因此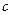 的最大值为
的最大值为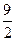 。
。略

练习册系列答案
相关题目
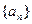 的前
的前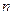 项和
项和 满足
满足
 的值; (2)求
的值; (2)求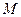 使下列不等式:
使下列不等式: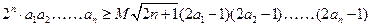
 成立?若存在,求出M的取值范围;若不存在,请说明理由
成立?若存在,求出M的取值范围;若不存在,请说明理由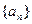 为等差数列, {bn}为等比数列, 且a1=b1=1,a2+a4=b3, b2b4=a3,分别求出{an}与{bn}的通项公式.
为等差数列, {bn}为等比数列, 且a1=b1=1,a2+a4=b3, b2b4=a3,分别求出{an}与{bn}的通项公式.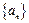 的各项均是正数,其前
的各项均是正数,其前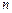 项和为
项和为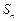 ,满足
,满足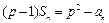 ,其中
,其中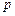 为正常数,且
为正常数,且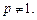
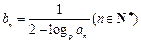 ,数列
,数列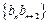 的前
的前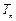 ,求证:
,求证: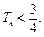
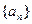 和
和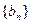 满足:
满足: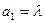 ,
,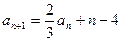 ,
,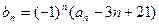 ,其中
,其中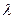 为实数,
为实数,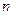 为正整数。
为正整数。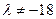 时,数列
时,数列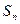 为数列
为数列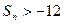 ?若存在,求
?若存在,求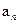 }从第一项开
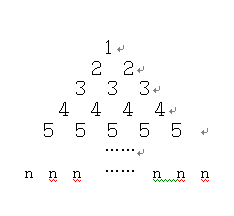
}从第一项开 始按照从上到下,从左到右的规律排列成如图所示的“三角阵”,即第一行是1个1,第二行是2个2,第三行是3个3,……,第n行是n个n(
始按照从上到下,从左到右的规律排列成如图所示的“三角阵”,即第一行是1个1,第二行是2个2,第三行是3个3,……,第n行是n个n( )
)
 1项
1项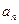 }的前
}的前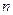 项和
项和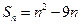 ,若它的第
,若它的第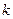 项满足
项满足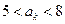 ,则
,则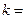 .
. 列,而1,y1,y2,8依次成等比数列,则△OP1P2的面
列,而1,y1,y2,8依次成等比数列,则△OP1P2的面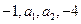 成等差数列,
成等差数列, 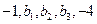 成等比数列,则
成等比数列,则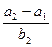 的值为________.
的值为________.